题目内容
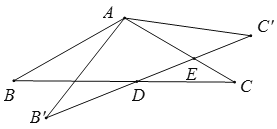
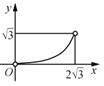
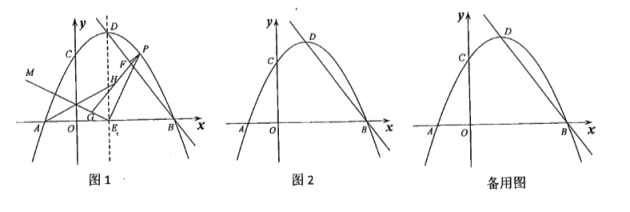
【题目】如图1,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 左侧),与
左侧),与![]() 轴交于点
轴交于点![]() ,点
,点![]() 抛物线的顶点.
抛物线的顶点.
(1)求直线![]() 的解析式;
的解析式;
(2)抛物线对称轴交![]() 轴于点
轴于点![]() ,
,![]() 为直线
为直线![]() 上方的抛物线上一动点,过点
上方的抛物线上一动点,过点![]() 作
作![]() 于点
于点![]() ,当线段
,当线段![]() 的长最大时,连接
的长最大时,连接![]() ,过点
,过点![]() 作射线
作射线![]() ,且
,且![]() ,点
,点![]() 为射线
为射线![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() 重合),连接
重合),连接![]() ,
,![]() 为
为![]() 中点,连接
中点,连接![]() ,求
,求![]() 的最小值;
的最小值;
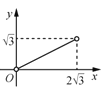
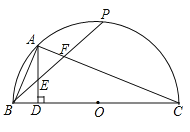
(3)如图2,平移抛物线,使抛物线的顶点![]() 在射线
在射线![]() 上移动,点
上移动,点![]() ,
,![]() 平移后的对应点分别为点
平移后的对应点分别为点![]() ,
,![]() ,
,![]() 轴上有一动点
轴上有一动点![]() ,连接
,连接![]() ,
,![]() ,
,![]() 是否能为等腰直角三角形?若能,请求出所有符合条件的
是否能为等腰直角三角形?若能,请求出所有符合条件的![]() 点的坐标;若不能,请说明理由.
点的坐标;若不能,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,![]() ,
,![]() .
.
【解析】
(1)首先求出B、D两点坐标,再利用待定系数法即可解决问题;
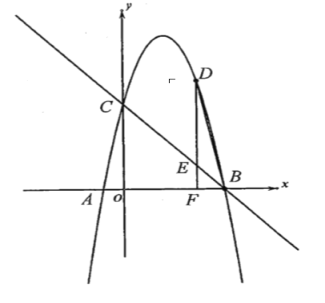
(2)如图2中,设P(m,-![]() m2+
m2+![]() m+2
m+2![]() ),连接PD、PB,作PQ⊥OB于Q.由题意欲求PF的最大值,易知当△PBD面积最大时,PF的值最大,由S△PBD=S△PDE+S△PEB-S△EDB,构建二次函数,求出PF的值最大时,点P的坐标为(2
),连接PD、PB,作PQ⊥OB于Q.由题意欲求PF的最大值,易知当△PBD面积最大时,PF的值最大,由S△PBD=S△PDE+S△PEB-S△EDB,构建二次函数,求出PF的值最大时,点P的坐标为(2![]() ,2
,2![]() ),易知点H的运动轨迹是线段PE的垂直平分线,易知当AH垂直PE的垂直平分线时,AH的值最小.利用相似三角形的性质求出AK,即可解决问题;
),易知点H的运动轨迹是线段PE的垂直平分线,易知当AH垂直PE的垂直平分线时,AH的值最小.利用相似三角形的性质求出AK,即可解决问题;
(3)如图3中,作MN⊥BD于N.当MN=BD时,存在△MB'D'为等腰直角三角形(只要D′或B′与N重合即可),易知H(0,4![]() ),由△HMN∽△DBE,可得
),由△HMN∽△DBE,可得![]() ,推出HM=
,推出HM=![]() ,推出OM=HM-OH=
,推出OM=HM-OH=![]() -4
-4![]() =
=![]() ,可得M(0,-
,可得M(0,-![]() ),点M关于H的对称点M′也满足条件,此时M′(0,
),点M关于H的对称点M′也满足条件,此时M′(0,![]() ),当M″是HM的中点时,M″是等腰三角形△M″B′D′的直角顶点;
),当M″是HM的中点时,M″是等腰三角形△M″B′D′的直角顶点;
(1)把![]() 代入,得
代入,得![]() ,解得:
,解得:![]() ,
,![]()
∴![]() ,
,![]()
∵![]()
∴![]()
设直线![]() 的解析式为
的解析式为![]()
把![]() ,
,![]() 代入,得:
代入,得: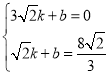 ,解得:
,解得: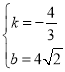
∴直线![]() 的解析式为
的解析式为![]()
(2)如图2中,设P(m,-![]() m2+
m2+![]() m+2
m+2![]() ),连接PD、PB,作PQ⊥OB于Q.
),连接PD、PB,作PQ⊥OB于Q.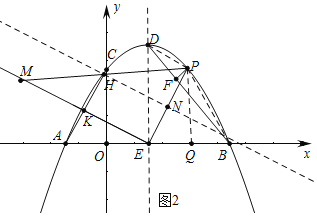
由题意欲求PF的最大值,易知当△PBD面积最大时,PF的值最大,
S△PBD=S△PDE+S△PEB-S△EDB=![]() ×
×![]() ×(m-
×(m-![]() )+
)+![]() ×2
×2![]() ×(-
×(-![]() m2+
m2+![]() m+2
m+2![]() )-
)-![]() ×2
×2![]() ×
×![]() =-
=-![]() (m-2
(m-2![]() )2+
)2+![]() ,
,
∵-![]() <0,
<0,
∴m=2![]() 时,△PBD的面积最大,PF的值最大,
时,△PBD的面积最大,PF的值最大,
∴此时P(2![]() ,2
,2![]() ),
),
易知点H的运动轨迹是线段PE的垂直平分线,
∴当AH垂直PE的垂直平分线时,AH的值最小,设AH交EM于K,
在Rt△EPQ中,PE=![]() ,
,
由△AKE∽△EQP,得到![]() ,
,
∴AK=![]() ,易知HK=NE=
,易知HK=NE=![]() PE=
PE=![]() ,
,
∴AH=AK+KH=![]() .
.
(3)如图3中,作MN⊥BD于N.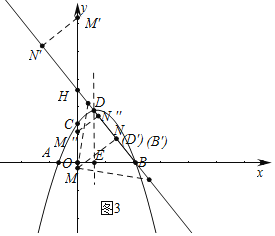
∵B(3![]() ,0),D(
,0),D(![]() ,
,![]() ),
),
∴BD=![]() ,
,
当MN=BD时,存在△MB'D'为等腰直角三角形(只要D′或B′与N重合即可),
∵直线BD的解析式为y=-![]() x+4
x+4![]() ,直线BD与y轴的交点H(0,4
,直线BD与y轴的交点H(0,4![]() ),
),
∵△HMN∽△DBE,
∴![]() ,
,
∴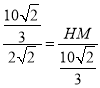 ,
,
∴HM=![]() ,
,
∴OM=HM-OH=![]() -4
-4![]() =
=![]() ,∴M(0,-
,∴M(0,-![]() ),
),
点M关于H的对称点M′也满足条件,此时M′(0,![]() ),
),
当M″是HM的中点时,M″是等腰三角形△M″B′D′的直角顶点,此时M″(0,![]() ),
),
综上所述,满足条件的点M的坐标为(0,-![]() )或(0,
)或(0,![]() )或(0,
)或(0,![]() ).
).

 阅读快车系列答案
阅读快车系列答案