ЬтФПФкШн
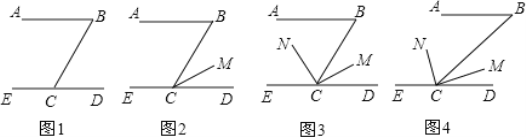
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуOдкжБЯпABЩЯЃЌНЋвЛИБжБНЧШ§НЧАхЕФжБНЧЖЅЕуЗХдкЕуOДІЃЌЦфжаЁЯOCD=60ЁуЃЌЁЯOEF=45ЁуЃЎБпOCЁЂOEдкжБЯпABЩЯЃЎ
ЃЈ1ЃЉШчЭМЃЈ1ЃЉЃЌШєCDКЭEFЯрНЛгкЕуGЃЌдђЁЯDGFЕФЖШЪ§ЪЧ______ЁуЃЛ
ЃЈ2ЃЉНЋЭМЃЈ1ЃЉжаЕФШ§НЧАхOCDШЦЕуOЫГЪБеыа§зЊ30ЁужСЭМЃЈ2ЃЉЮЛжУ
ЂйШєНЋШ§НЧАхOEFШЦЕуOЫГЪБеыа§зЊ180ЁуЃЌдкДЫЙ§ГЬжаЃЌЕБЁЯCOE=ЁЯEOD=ЁЯDOFЪБЃЌЧѓЁЯAOEЕФЖШЪ§ЃЛ
ЂкШєНЋШ§НЧАхOEFШЦЕуOвдУПУы4ЁуЕФЫйЖШЫГЪБеыа§зЊ180ЁуЃЌгыДЫЭЌЪБЃЌНЋШ§НЧАхOCDШЦЕуOвдУПУы1ЁуЕФЫйЖШЫГЪБеыа§зЊЃЌЕБШ§НЧАхOEFа§зЊЕНжеЕуЮЛжУЪБЃЌШ§НЧАхOCDвВЭЃжЙа§зЊЃЎЩша§зЊЪБМфЮЊtУыЃЌЕБODЁЭEFЪБЃЌЧѓtЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉ15ЃЛЃЈ2ЃЉЂйЕБЁЯCOE=ЁЯEOD=ЁЯDOFЪБЃЌЁЯAOE=75ЁуЃЛЂкЕБODЁЭEFЪБЃЌtЕФжЕЮЊ25ЃЎ
ЁОНтЮіЁП
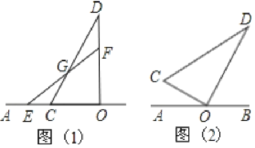
ЃЈ1ЃЉИљОнШ§НЧаЮЭтНЧЕФаджЪМДПЩЕУЕННсТлЃЛ
ЃЈ2ЃЉЂйШчЭМ2ЃЌИљОнвбжЊЬѕМўЧѓГіЁЯCOE=ЁЯEOD=45ЁуЃЌЕУЕНЁЯAOE=ЁЯAOC+ЁЯCOE=30Ёу+45Ёу=75ЁуЃЌЕБЁЯCOE=ЁЯEOD=ЁЯDOFЪБЃЌЧѓЕУНсТлЃЛЂкИљОнДЙжБЕФЖЈвхЕУЕНODЁЭEFЃЌЕУЕНЁЯOHE=90ЃЌСаЗНГЬЧѓЕУНсТлЃЎ
ЃЈ1ЃЉЁпЁЯEFO=45ЁуЃЌЁЯD=30ЁуЃЌ
ЁрЁЯDGF=ЁЯEFO-ЁЯD=45Ёу-30Ёу=15ЁуЃЌ
ЙЪД№АИЮЊЃК15ЃЛ
ЃЈ2ЃЉЂйШчЭМ2ЃЌ
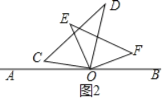
ЁпЁЯCOE=ЁЯEOD=ЁЯDOFЃЌЁЯCOE+ЁЯEOD=ЁЯCODЃЌЁЯCOD=90ЁуЃЌ
ЁрЁЯCOE=ЁЯEOD=45ЁуЃЌ
ЁрЁЯAOE=ЁЯAOC+ЁЯCOE=30Ёу+45Ёу=75ЁуЃЌ
ЕБЁЯCOE=ЁЯEOD=ЁЯDOFЪБЃЌЁЯAOE=75ЁуЃЛ
ЂкЁпЁЯAOE=4tЁуЃЌЁЯAOC=30Ёу+tЁуЃЌШчЭМ3ЃЌ
ЁпODЁЭEFЃЌ
ЁрЁЯOHE=90ЃЌ
ЁпЁЯE=45ЁуЃЌЁЯCOD=90ЁуЃЌ
ЁрЁЯCOE=45ЁуЃЌ
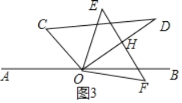
ЁрЁЯAOE-ЁЯAOC=ЁЯCOE=45ЁуЃЌ
МД4t-ЃЈ30+tЃЉ=45ЃЌ
Ёрt=25ЃЌ
ЁрЕБODЁЭEFЪБЃЌtЕФжЕЮЊ25ЃЎ