题目内容
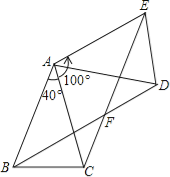
【题目】如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.设点N的坐标为(m,n).

(1)若建立平面直角坐标系,满足原点在线段BD上,点B(﹣1,0),A(0,1).且BM=t(0<t≤2),则点D的坐标为 ,点C的坐标为 ;请直接写出点N纵坐标n的取值范围是 ;
(2)若正方形的边长为2,求EC的长,以及AM+BM+CM的最小值.(提示:连结MN,![]() ,
,![]() )
)
【答案】(1)D(1,0),C(0,﹣1);0<n≤![]() ;(2)EC=
;(2)EC=![]() +
+![]() ,AM+BM+CM的最小值为
,AM+BM+CM的最小值为![]() +
+![]()
【解析】
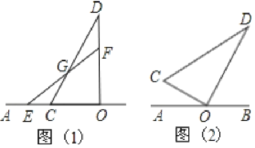
(1)如图1,以直线BD为x轴,直线AC为y轴,建立平面直角坐标系,根据正方形的性质得到OA=OB=OC=OD,由点B(1,0),A(0,1),于是得到D(1,0),C(0,1);过N作NH⊥BD于h,根据旋转的性质得到∠NBH=60°,BM=BN,求得NH=![]() BN=
BN=![]() t,于是得到结论;
t,于是得到结论;
(2)如图所示,连接MN,过E作EH⊥BC,交CB的延长线于H,由旋转的性质得到BM=BN,∠NBM=60°,求得△BMN是等边三角形,求得MN=BM,根据等边三角形的性质得到BE=BA,∠ABE=60°,求得∠ABM=∠EBN,根据全等三角形的性质得到AM=EN,求得AM+BM+CM=EN+MN+CM,当E,N,M,C在同一直线上时,AM+BM+CN的最小值是CE的长,利用勾股定理即可得到结论.
解:(1)如图1,以直线BD为x轴,直线AC为y轴,建立平面直角坐标系,
∵四边形ABCD是正方形,
∴OA=OB=OC=OD,
∵点B(﹣1,0),A(0,1),
∴D(1,0),C(0,﹣1);
过N作NH⊥BD于h,
∴∠NHB=90°,
∵将BM绕点B逆时针旋转60°得到BN,
∴∠NBH=60°,BM=BN,
∴NH=![]() BN=
BN=![]() t,
t,
∵0<t≤2,
∴点N纵坐标n的取值范围是0<n≤![]() ;
;
(2)如图2所示,连接MN,过E作EH⊥BC,交CB的延长线于H,
由旋转可得,BM=BN,∠NBM=60°,
∴△BMN是等边三角形,
∴MN=BM,
∵△ABE是等边三角形,
∴BE=BA,∠ABE=60°,
∴∠ABM=∠EBN,
∴△ABM≌△EBN(SAS),
∴AM=EN,
∴AM+BM+CM=EN+MN+CM,
∴当E,N,M,C在同一直线上时,AM+BM+CN的最小值是CE的长,
又∵∠ABE=60°,∠ABH=90°,
∴∠EBH=30°,
∴Rt△EBH中,EH=![]() EB=
EB=![]() ×2=1,
×2=1,
∴BH=![]() =
=![]() =
=![]() ,
,
∴CH=2+![]() ,
,
∴Rt△CEH中,CE=![]() =
=![]() =
=![]() =
=![]() ;
;
∴AM+BM+CM的最小值为![]() +
+![]() .
.