Question

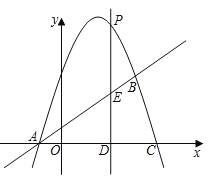
【题目】如图是抛物线y＝ax2+bx+c（a≠0）的部分图象，其顶点坐标为（1，5）且与x轴的一个交点在（3，0）和（4，0）之间，则下列结论：①a﹣b+c＞0；②2a+b＝0；③b2﹣4ac＞0；④一元二次方程ax2+bx+c＝5有两个不相等的实数根．其中正确结论的个数是（　　）

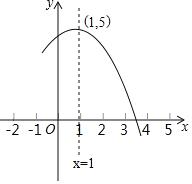
A.1B.2C.3D.4

Answer 1

【答案】C

【解析】

根据x＝﹣1时，y＞0，可判断①；根据对称轴x＝﹣＝1，可判断②；根据抛物线与x轴有两个交点，可知△＞0，进而判断③；根据抛物线的顶点坐标为（1，5），直线y＝5与抛物线只有一个交点，推出一元二次方程ax2+bx+c＝5有两个相等的实数根，由此即可判断④．

解：由图象可知，当x＝﹣1时，y＞0，

∴a﹣b+c＞0，故①正确；

∵抛物线的对称轴为x＝1，

∴﹣＝1，

∴﹣b＝2a，即2a+b＝0，故②正确；

∵抛物线与x轴有两个交点，

∴△＝b2﹣4ac＞0，故③正确；

∵抛物线的顶点坐标为（1，5），

∴直线y＝5与抛物线只有一个交点，

∴一元二次方程ax2+bx+c＝5有两个相等的实数根，故④错误．

故选：C．