题目内容
【题目】为测量某特种车辆的性能,研究制定了行驶指数![]() ,而
,而![]() 的大小与平均速度
的大小与平均速度![]() 和行驶路程
和行驶路程![]() 有关(不考虑其他因素),
有关(不考虑其他因素),![]() 由两部分的和组成,一部分与
由两部分的和组成,一部分与![]() 成正比,另一部分与
成正比,另一部分与![]() 成正比.在实验中得到了表格中的数据:
成正比.在实验中得到了表格中的数据:
速度 |
|
|
路程 |
|
|
指数 |
|
|
(1)用含![]() 和
和![]() 的式子表示
的式子表示![]() ;
;
(2)当行驶指数为![]() ,而行驶路程为
,而行驶路程为![]() 时,求平均速度的值;
时,求平均速度的值;
(3)当行驶路程为![]() 时,若行驶指数值最大,求平均速度的值.
时,若行驶指数值最大,求平均速度的值.
【答案】(1)![]() ;(2)50 km/h;(3)90 km/h.
;(2)50 km/h;(3)90 km/h.
【解析】
(1)设K=mv2+nsv,则P=mv2+nsv+1000,利用待定系数法求解可得;
(2)将P=500代入(1)中解析式,解方程可得;
(3)将s=180代入解析式后,配方成顶点式可得最值情况.
解:(1)设K=mv2+nsv,则P=mv2+nsv+1000,
由题意得: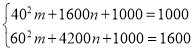 ,
,
整理得:![]() ,
,
解得:![]() ,
,
则P=﹣v2+sv+1000;
(2)根据题意得﹣v2+40v+1000=500,
整理得:v2﹣40v﹣500=0,
解得:v=﹣10(舍)或v=50,
答:平均速度为50km/h;
(3)当s=180时,P=﹣v2+180v+1000=﹣(v﹣90)2+9100,
∴当v=90时,P最大=9100,
答:若行驶指数值最大,平均速度的值为90km/h.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | … | ﹣6 | 0 | 4 | 6 | 6 | … |
给出下列说法:
①抛物线与y轴的交点为(0,6);
②抛物线的对称轴在y轴的左侧;
③抛物线一定经过(3,0)点;
④在对称轴左侧y随x的增大而减增大.
从表中可知,其中正确的个数为( )
A.4 B.3 C.2 D.1