题目内容
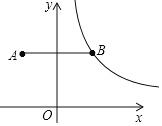
【题目】如图,![]() 的顶点
的顶点![]() 在双曲线
在双曲线![]() 的图象上,直角边
的图象上,直角边![]() 在
在![]() 轴上,
轴上,![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,
,![]() ,则
,则![]() 的值是( )
的值是( )

A. 4![]() B. -4
B. -4![]() C. 2
C. 2![]() D. -2
D. -2![]()
【答案】B
【解析】
根据三角形外角性质得∠OAC=∠AOB﹣∠ACB=30°,易得OA=OC=4,然后再Rt△AOB中利用含30度的直角三角形三边的关系得到OB=![]() OC=2,AB=
OC=2,AB=![]() OB=2
OB=2![]() ,则可确定A点坐标为(﹣2,2
,则可确定A点坐标为(﹣2,2![]() ),最后把A点坐标代入反比例函数解析式y=
),最后把A点坐标代入反比例函数解析式y=![]() 中即可得到k的值.
中即可得到k的值.
∵∠ACB=30°,∠AOB=60°,∴∠OAC=∠AOB﹣∠ACB=30°,∴∠OAC=∠ACO,∴OA=OC=4.
在△AOB中,∠ABC=90°,∠AOB=60°,OA=4,∴∠OAB=30°,∴OB=![]() OC=2,∴AB=
OC=2,∴AB=![]() OB=2
OB=2![]() ,∴A点坐标为(﹣2,2
,∴A点坐标为(﹣2,2![]() ),把A(﹣2,2
),把A(﹣2,2![]() )代入y=
)代入y=![]() 得:k=﹣2×2
得:k=﹣2×2![]() =﹣4
=﹣4![]() .
.
故选B.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
【题目】为测量某特种车辆的性能,研究制定了行驶指数![]() ,而
,而![]() 的大小与平均速度
的大小与平均速度![]() 和行驶路程
和行驶路程![]() 有关(不考虑其他因素),
有关(不考虑其他因素),![]() 由两部分的和组成,一部分与
由两部分的和组成,一部分与![]() 成正比,另一部分与
成正比,另一部分与![]() 成正比.在实验中得到了表格中的数据:
成正比.在实验中得到了表格中的数据:
速度 |
|
|
路程 |
|
|
指数 |
|
|
(1)用含![]() 和
和![]() 的式子表示
的式子表示![]() ;
;
(2)当行驶指数为![]() ,而行驶路程为
,而行驶路程为![]() 时,求平均速度的值;
时,求平均速度的值;
(3)当行驶路程为![]() 时,若行驶指数值最大,求平均速度的值.
时,若行驶指数值最大,求平均速度的值.