题目内容
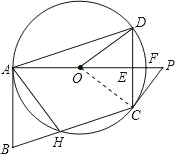
【题目】如图,⊙O过ABCD的三顶点A、D、C,边AB与⊙O相切于点A,边BC与⊙O相交于点H,射线AD交边CD于点E,交⊙O于点F,点P在射线AO上,且∠PCD=2∠DAF.
(1)求证:△ABH是等腰三角形;
(2)求证:直线PC是⊙O的切线;
(3)若AB=2,AD=![]() ,求⊙O的半径.
,求⊙O的半径.

【答案】(1)证明参见解析;(2)证明参见解析;(3)![]() .
.
【解析】
试题分析:(1)要想证明△ABH是等腰三角形,只需要根据平行四边形的性质可得∠B=∠ADC,再根据圆内接四边形的对角互补,可得∠ADC+∠AHC=180°,再根据邻补角互补,可知∠AHC+∠AHB=180°,从而可以得到∠ABH和∠AHB的关系,从而可以证明结论成立;(2)要证直线PC是⊙O的切线,只需要连接OC,证明∠OCP=90°即可,根据平行四边形的性质和边AB与⊙O相切于点A,可以得到∠AEC的度数,又∠PCD=2∠DAF,∠DOF=2∠DAF,∠COE=∠DOF,通过转化可以得到∠OCP的度数,从而可以证明结论;(3)根据题意和(1)(2)可以得到∠AED=90°,由平行四边形的性质和勾股定理,由AB=2,AD=![]() ,可以求得半径的长.
,可以求得半径的长.
试题解析:(1)证明:∵四边形ADCH是圆内接四边形,∴∠ADC+∠AHC=180°,又∵∠AHC+∠AHB=180°,∴∠ADC=∠AHB,∵四边形ABCD是平行四边形,∴∠ADC=∠B,∴∠AHB=∠B,∴AB=AH,∴△ABH是等腰三角形;(2)证明:连接OC,如右图所示,∵边AB与⊙O相切于点A,∴BA⊥AF,∵四边形ABCD是平行四边形,∴AB∥CD,∴CD⊥AF,又∵FA经过圆心O,∴弧DF=弧CF,∠OEC=90°,∴∠COF=2∠DAF,又∵∠PCD=2∠DAF,∴∠COF=∠PCD,∵∠COF+∠OCE=90°,∴∠PCD+∠OCE=90°,即∠OCP=90°,
∴直线PC是⊙O的切线;(3)∵四边形ABCD是平行四边形,∴DC=AB=2,∵FA⊥CD,∴DE=CE=1,∵∠AED=90°,AD=![]() ,DE=1,∴AE=
,DE=1,∴AE=![]() ,设⊙O的半径为r,则OA=OD=r,OE=AE﹣OA=4﹣r,∵∠OED=90°,DE=1,∴r2=(4﹣r)2+12,解得,r=
,设⊙O的半径为r,则OA=OD=r,OE=AE﹣OA=4﹣r,∵∠OED=90°,DE=1,∴r2=(4﹣r)2+12,解得,r=![]() ,即⊙O的半径是
,即⊙O的半径是![]() .
.

【题目】学生经常玩手机游戏会影响学习和生活,某校调查了20名同学某一周玩手机游戏的次数,调查结果如表所示,那么这20名同学玩手机游戏的平均数为( )
次数 | 2 | 4 | 5 | 8 |
人数 | 2 | 2 | 10 | 6 |
A. 5 B. 5.5 C. 6 D. 6.5