Question

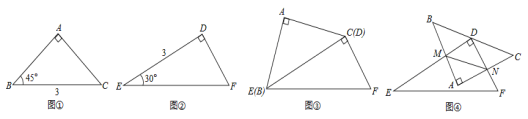
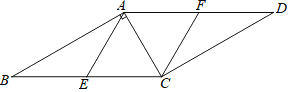
【题目】如图，已知点E，F分别是平行四边形ABCD的边BC，AD上的中点．

（1）AE与CF的关系是　 　，请证明；

（2）若∠BAC＝　 　°时，四边形AECF是菱形，请说明理由．

Answer 1

【答案】（1）AE＝CF，AE//CF，证明见解析；（2）90，理由见解析.

【解析】

（1）通过证明四边形AECF是平行四边形，可得AE＝CF，AE//CF；

（2）由直角三角形的性质可得AE＝CE，且四边形AECF是平行四边形，可得四边形AECF是菱形．

解：（1）AE＝CF，AE//CF，理由如下：

∵四边形ABCD是平行四边形，

∴AD∥BC，AD＝BC．

∵点E，F分别是平行四边形ABCD的边BC，AD上的中点．

∴AF＝CE，且AF∥CE，

∴四边形AECF是平行四边形，

∴AE＝CF，AE//CF，

故答案为：AE＝CF，AE//CF；

（2）90°，理由如下：

当∠BAC＝90°时

∵点E是BC边的中点，

∴AE＝CE＝BE＝BC

∵四边形AECF是平行四边形

∴平行四边形AECF是菱形．