Question

【题目】如图1，在平面直角坐标系中，已知A（a，b），且a.b满足，

（1）求A点的坐标及线段OA的长度；（2）点P为x轴正半轴上一点，且△AOP是等腰三角形，求P点的坐标；

（3）如图2，若B（1，0），C（0，－3），试确定∠ACO+∠BCO的值是否发生变化，若不变，求其值；若变化，请求出变化范围。

Answer 1

【答案】（1）；（2）P(,0)或P(4,0)、P（，0）；（3）45.

【解析】

（1）先由二次根式有意义的条件得出a的值，再代入等式得出b的值，从而得出点A的坐标，继而利用两点间的距离公式可得OA的长；

（2）分OA=OP、AO=AP、PO=PA三种情况，利用等腰三角形的性质逐一求解可得；

（3）在x轴负半轴上取一点，使得OD=OB=1，知点B与点D关于y轴对称，据此得∠BCO=∠DCO，根据两点间的距离公式知AD2=10，CD2=10，AC2=20，依据勾股定理逆定理判断出△ACD是等腰直角三角形，利用∠ACO+∠BCO=∠ACO+∠DCO=∠ACD可得答案．

解：

（1）∵，

∴a=2，

则b=1，

∴A（2，1），

则OA=＝；

（2）当OA=OP时，P（，0）；

当AO=AP时，如图1，作AH⊥x轴于点H，

则OH=PH=2，

∴OP=4，

∴P（4，0）；

当P′O=P′A时，设P′O=P′A=x，则P′H=2-x，

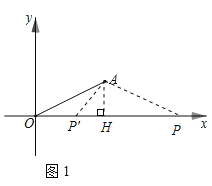
由AP′2=P′H2+AH2得（2-x）2+12=x2，

解得：x=，

∴P（，0）．

（3）如图2，在x轴负半轴上取一点，使得OD=OB=1，

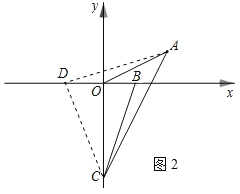
则点B与点D关于y轴对称，

∴∠BCO=∠DCO，

∵A（2，1），D（-1，0），C（0，-3），

∴AD2=32+12=10，CD2=12+32=10，AC2=22+42=20，

∴AD2+CD2=AC2，且AD=CD，

∴△ACD是等腰直角三角形，

则∠ACO+∠BCO=∠ACO+∠DCO=∠ACD=45°．