题目内容
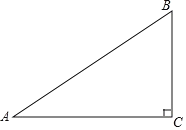
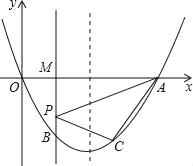
【题目】如图,抛物线y=x2﹣2mx(m>0)与x轴的另一个交点为A,过P(1,﹣m)作PM⊥x轴于点M,交抛物线于点B.点B关于抛物线对称轴的对称点为C.
(1)若m=2,求点A和点C的坐标;
(2)令m>1,连接CA,若△ACP为直角三角形,求m的值;
(3)在坐标轴上是否存在点E,使得△PEC是以P为直角顶点的等腰直角三角形?若存在,求出点E的坐标;若不存在,请说明理由.
【答案】(1)A(4,0),C(3,﹣3);(2) m=![]() ;(3) E点的坐标为(2,0)或(
;(3) E点的坐标为(2,0)或(![]() ,0)或(0,﹣4);
,0)或(0,﹣4);
【解析】
方法一:(1)m=2时,函数解析式为y=![]() ,分别令y=0,x=1,即可求得点A和点B的坐标, 进而可得到点C的坐标;
,分别令y=0,x=1,即可求得点A和点B的坐标, 进而可得到点C的坐标;
(2) 先用m表示出P, A C三点的坐标,分别讨论∠APC=![]() ,∠ACP=
,∠ACP=![]() ,∠PAC=
,∠PAC=![]() 三种情况, 利用勾股定理即可求得m的值;
三种情况, 利用勾股定理即可求得m的值;
(3) 设点F(x,y)是直线PE上任意一点,过点F作FN⊥PM于N,可得Rt△FNP∽Rt△PBC,
NP:NF=BC:BP求得直线PE的解析式,后利用△PEC是以P为直角顶点的等腰直角三角形求得E点坐标.
方法二:(1)同方法一.
(2) 由△ACP为直角三角形, 由相互垂直的两直线斜率相乘为-1,可得m的值;
(3)利用△PEC是以P为直角顶点的等腰直角三角形,分别讨论E点再x轴上,y轴上的情况求得E点坐标。
方法一:
解: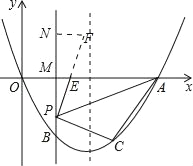
(1)若m=2,抛物线y=x2﹣2mx=x2﹣4x,
∴对称轴x=2,
令y=0,则x2﹣4x=0,
解得x=0,x=4,
∴A(4,0),
∵P(1,﹣2),令x=1,则y=﹣3,
∴B(1,﹣3),
∴C(3,﹣3).
(2)∵抛物线y=x2﹣2mx(m>1),
∴A(2m,0)对称轴x=m,
∵P(1,﹣m)
把x=1代入抛物线y=x2﹣2mx,则y=1﹣2m,
∴B(1,1﹣2m),
∴C(2m﹣1,1﹣2m),
∵PA2=(﹣m)2+(2m﹣1)2=5m2﹣4m+1,
PC2=(2m﹣2)2+(1﹣m)2=5m2﹣10m+5,
AC2=1+(1﹣2m)2=2﹣4m+4m2,
∵△ACP为直角三角形,
∴当∠ACP=90°时,PA2=PC2+AC2,
即5m2﹣4m+1=5m2﹣10m+5+2﹣4m+4m2,整理得:4m2﹣10m+6=0,
解得:m=![]() ,m=1(舍去),
,m=1(舍去),
当∠APC=90°时,PA2+PC2=AC2,
即5m2﹣4m+1+5m2﹣10m+5=2﹣4m+4m2,整理得:6m2﹣10m+4=0,
解得:m=![]() ,m=1,
,m=1,![]() 和1都不符合m>1,
和1都不符合m>1,
故m=![]() .
.
(3)设点F(x,y)是直线PE上任意一点,过点F作FN⊥PM于N,
∵∠FPN=∠PCB,∠PNF=∠CBP=90°,
∴Rt△FNP∽Rt△PBC,
∴NP:NF=BC:BP,即![]() =
=![]() ,
,
∴y=2x﹣2﹣m,
∴直线PE的解析式为y=2x﹣2﹣m.
令y=0,则x=1+![]() ,
,
∴E(1+![]() m,0),
m,0),
∴PE2=(﹣m)2+(![]() m)2=
m)2=![]() ,
,
∴![]() =5m2﹣10m+5,解得:m=2,m=
=5m2﹣10m+5,解得:m=2,m=![]() ,
,
∴E(2,0)或E(![]() ,0),
,0),
∴在x轴上存在E点,使得△PEC是以P为直角顶点的等腰直角三角形,此时E(2,0)或E(![]() ,0);
,0);
令x=0,则y=﹣2﹣m,
∴E(0,﹣2﹣m)
∴PE2=(﹣2)2+12=5
∴5m2﹣10m+5=5,解得m=2,m=0(舍去),
∴E(0,﹣4)
∴y轴上存在点E,使得△PEC是以P为直角顶点的等腰直角三角形,此时E(0,﹣4),
∴在坐标轴上是存在点E,使得△PEC是以P为直角顶点的等腰直角三角形,E点的坐标为(2,0)或(![]() ,0)或(0,﹣4);
,0)或(0,﹣4);
方法二:
(1)略.
(2)∵P(1,﹣m),
∴B(1,1﹣2m),
∵对称轴x=m,
∴C(2m﹣1,1﹣2m),A(2m,0),
∵△ACP为直角三角形,
∴AC⊥AP,AC⊥CP,AP⊥CP,
①AC⊥AP,∴KAC×KAP=﹣1,且m>1,
∴![]() ,m=﹣1(舍)
,m=﹣1(舍)
②AC⊥CP,∴KAC×KCP=﹣1,且m>1,
∴![]() =﹣1,∴m=
=﹣1,∴m=![]() ,
,
③AP⊥CP,∴KAP×KCP=﹣1,且m>1,
∴![]() =﹣1,∴m=
=﹣1,∴m=![]() (舍)
(舍)
(3)∵P(1,﹣m),C(2m﹣1,1﹣2m),
∴KCP=![]() ,
,
△PEC是以P为直角顶点的等腰直角三角形,
∴PE⊥PC,∴KPE×KCP=﹣1,∴KPE=2,
∵P(1,﹣m),
∴lPE:y=2x﹣2﹣m,
∵点E在坐标轴上,
∴①当点E在x轴上时,
E(![]() ,0)且PE=PC,
,0)且PE=PC,
∴(1﹣![]() )2+(﹣m)2=(2m﹣1﹣1)2+(1﹣2m+m)2,
)2+(﹣m)2=(2m﹣1﹣1)2+(1﹣2m+m)2,
∴![]() m2=5(m﹣1)2,
m2=5(m﹣1)2,
∴m1=2,m2=![]() ,
,
∴E1(2,0),E2(![]() ,0),
,0),
②当点E在y轴上时,E(0,﹣2﹣m)且PE=PC,
∴(1﹣0)2+(﹣m+2+m)2=(2m﹣1﹣1)2+(1﹣2m+m)2,
∴1=(m﹣1)2,
∴m1=2,m2=0(舍),
∴E(0,4),
综上所述,(2,0)或(![]() ,0)或(0,﹣4).
,0)或(0,﹣4).

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案