题目内容
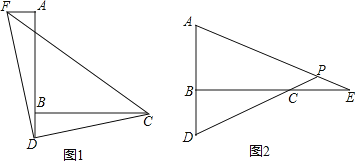
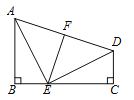
【题目】如图:AB⊥BC,DC⊥BC,E在BC上,AB=EC,BE=CD,EF⊥AD于F.
(1)求证:F是AD中点;
(2)求∠AEF的度数.
【答案】(1)证明见解析;(2)45°
【解析】试题分析:(1)由题意,AB⊥BC,DC⊥BC,AB=EC,BE=CD,可证△ABE≌△ECD,可证AE=ED,且EF⊥AD,即可得证F是AD是中点.
(2)由(1)可推出,△AED为等腰直角三角形,所以∠AEF=45°.
试题解析:由题意,AB⊥BC,DC⊥BC,AB=EC,BE=CD,
所以△ABE≌△ECD,
所以AE=ED,
又EF⊥AD,
即可得证F是AD是中点;
(2)由(1)得,∠AEB+∠CED=90°;
所以∠AED=90°,
所以△AED为等腰直角三角形,
所以∠AEF=45°.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目