Question

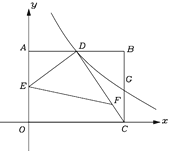
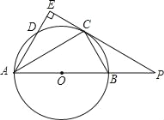
【题目】如图，AB是半圆O的直径，点C为⊙O上一点，AE和过点C的切线互相垂直，垂足为E，AE交⊙O于点D，直线EC交AB的延长线于点P，连接AC，BC，，AD=3．给出下列结论：①AC平分∠BAD；②△ABC∽△ACE；③AB=3PB；④S△ABC=5，其中正确的是__________（写出所有正确结论的序号）．

Answer 1

【答案】①②③④

【解析】

①首先连接OC，由PE是⊙O的切线，AE和过点C的切线互相垂直，可证得OC∥AE，又由OA=OC，易证得∠DAC=∠OAC，即可得AC平分∠BAD；

②根据两角相等两三角形相似即可判断；

③由AB是⊙O的直径，PE是切线，可证得∠PCB=∠PAC，即可证得△PCB∽△PAC，然后由相似三角形的对应边成比例与PB：PC=1：2，即可求得答案；

④首先过点O作OH⊥AD于点H，则AH=AD=，四边形OCEH是矩形，即可得AE=+OC，由OC∥AE，可得△PCO∽△PEA，然后由相似三角形的对应边成比例，求得OC的长，再由△PBC∽△PCA，证得AC=2BC，然后在Rt△ABC中，AC2+BC2=AB2，可得（2BC）2+BC2=52，即可求得BC的长，继而求得答案；

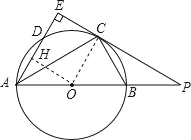
连接OC，

∵PE是⊙O的切线，

∴OC⊥PE，

∵AE⊥PE，

∴OC∥AE，

∴∠DAC=∠OCA，

∵OA=OC，

∴∠OCA=∠OAC，

∴∠DAC=∠OAC，

∴AC平分∠BAD；故①正确，

∵AB是直径，

∴∠ACB=∠AEC=90°，

∵∠CAE=∠CAB，

∴△AEC∽△ACB，故②正确，

∵∠BAC+∠ABC=90°，

∵OB=OC，

∴∠OCB=∠ABC，

∵∠PCB+∠OCB=90°，

∴∠PCB=∠PAC，

∵∠P是公共角，

∴△PCB∽△PAC，

∴，

∴PC2=PBPA，

∵PB：PC=1：2，

∴PC=2PB，

∴PA=4PB，

∴AB=3PB；故③正确

过点O作OH⊥AD于点H，则AH=AD=，四边形OCEH是矩形，

∴OC=HE，

∴AE=+OC，

∵OC∥AE，

∴△PCO∽△PEA，

∴，

∵AB=3PB，AB=2OB，

∴OB=PB，

∴，

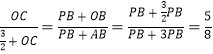∴OC=，

∴AB=5，

∵△PBC∽△PCA，

∴，

∴AC=2BC，

在Rt△ABC中，AC2+BC2=AB2，

∴（2BC）2+BC2=52，

∴BC=，

∴AC=2，

∴S△ABC=ACBC=5．故④正确，

故答案为：①②③④．