题目内容
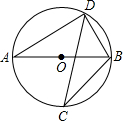如图，若AB是⊙0的直径，CD是⊙O的弦，∠C=30°，BD=1，则⊙O的半径是（ ）分析：先根据圆周角定理求出∠A及∠ADB的度数，再由直角三角形的性质即可得出结论．
解答：解：∵∠A与∠C是同弧所对的圆周角，∠C=30°，
∴∠A=30°，
∵AB是⊙O的直径，
∴△ABD是直角三角形，
∴AB=2BD=2×1=2，
∴OB=
AB=
×2=1．
故答案为：1．
∴∠A=30°，
∵AB是⊙O的直径，
∴△ABD是直角三角形，
∴AB=2BD=2×1=2，
∴OB=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为：1．
点评：本题考查的是圆周角定理及直角三角形的性质，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解答此题的关键．
练习册系列答案
相关题目
3、如图，若AB是⊙0的直径，CD是⊙O的弦，∠ABD=58°，则∠BCD=（ ）
（2013•益阳）如图，若AB是⊙O的直径，AB=10cm，∠CAB=30°，则BC=
（2013•宜春模拟）如图，若AB是⊙O的弦，CD是⊙O的直径，∠ABD=28°，则∠ADC的度数为
如图，若AB是⊙O的直径，CD是⊙O的弦，∠ABD=58°，则∠C的度数为（ ）
（2013•安溪县质检）如图，若AB是⊙O的直径，弦CD交AB于点E，∠DCB=34°，∠CDB=40°，则∠AEC=（ ）