题目内容
（2013•宜春模拟）如图，若AB是⊙O的弦，CD是⊙O的直径，∠ABD=28°，则∠ADC的度数为62°
62°
．分析：连接OA，先根据圆周角定理求出∠AOD的度数，再根据等腰三角形的性质即可得出结论．
解答：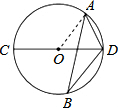
解：连接OA，
∵∠ABD=28°，
∴∠AOD=2∠ABD=56°，
∵OA=OD，
∴∠ADC=
=
=62°．
故答案为：62°．
解：连接OA，∵∠ABD=28°，
∴∠AOD=2∠ABD=56°，
∵OA=OD，
∴∠ADC=
| 180°-∠AOD |
| 2 |
| 180°-56° |
| 2 |
故答案为：62°．
点评：本题考查的是圆周角定理，根据题意作出辅助线，构造出圆心角是解答此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
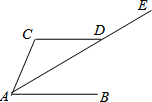（2013•宜春模拟）如图所示，已知AE平分∠BAC交CD于点D，且AB∥CD，∠C=100°，则∠EAC为（ ）