Question

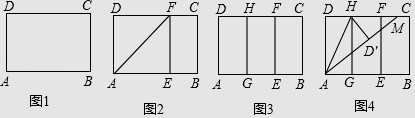
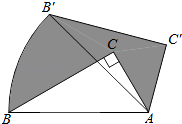
【题目】如图，BD=CD，∠ABD=∠ACD=90°，点E、F分别在AB、AC上，若ED平分∠BEF．

（1）求证：FD平分∠EFC．

（2）若EF=4，AF=6，AE=5，求BE和CF的和的长．

Answer 1

【答案】（1）证明见解析；（2）4．

【解析】试题分析：（1）过D作DM⊥EF，已知ED平分∠BEF，根据角平分线的性质定理可得BD=DM，又因BD=CD，可得DC=DM，根据角平分线的判定定理即可得FD平分∠EFC；（2）因为ED平分∠BEF，即可得∠BDE=∠MDE，利用SAS即可判定△BDE≌△MDE，根据全等三角形的性质即可得EB=EM，同理即可证得CF=MF，根据EF=BE+CF即可求得EF的长．

试题解析：

证明：（1）过D作DM⊥EF，

∵ED平分∠BEF，

∴BD=DM，

∵BD=CD，

∴DC=DM，

∴FD平分∠EFC；

（2）∵ED平分∠BEF，

∴∠BDE=∠MDE，

在△BDE和△MDE中，，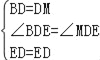

∴△BDE≌△MDE（SAS），

∴EB=EM，

同理CF=MF，

∴EF=BE+CF=4．