题目内容
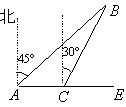
【题目】如图,将含60°角的直角三角板ABC绕顶点A顺时针旋转45°度后得到△AB′C′,点B经过的路径为弧BB′,若∠BAC=60°,AC=1,则图中阴影部分的面积是( ) 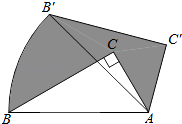
A.![]()
B.![]()
C.![]()
D.π
【答案】A
【解析】解:如图,∵在Rt△ABC中,∠ACB=90°,∠BAC=60°,AC=1, ∴BC=ACtan60°=1× ![]() =
= ![]() ,AB=2
,AB=2
∴S△ABC= ![]() ACBC=
ACBC= ![]() .
.
根据旋转的性质知△ABC≌△AB′C′,则S△ABC=S△AB′C′ , AB=AB′.
∴S阴影=S扇形ABB′+S△AB′C′﹣S△ABC
= ![]()
= ![]() .
.
故选:A.
【考点精析】根据题目的已知条件,利用扇形面积计算公式和旋转的性质的相关知识可以得到问题的答案,需要掌握在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2);①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目