题目内容
【题目】综合题。
(1)计算:(3﹣π)0﹣ ![]() +|3﹣
+|3﹣ ![]() |+(tan30°)﹣1
|+(tan30°)﹣1
(2)定义新运算:对于任意实数a,b,都有a⊕b=a(a﹣b)+1,等式右边是通常的加法、减法及乘法运算. 比如:2⊕5=2×(2﹣5)+1
=2×(﹣3)+1
=﹣6+1
=﹣5
若3⊕x的值小于13,求x的取值范围,并在如图所示的数轴上表示出来.![]()
【答案】
(1)解:原式=1﹣3+3﹣ ![]() +
+ ![]() =1
=1
(2)解:根据题中的新定义化简得:3⊕x=3(3﹣x)+1<13,
解得:x>﹣1,
在数轴上表示,如图所示:
![]()
【解析】(1)原式利用零指数幂、负整数指数幂法则,算术平方根定义,以及绝对值的代数意义化简即可得到结果;(2)根据题中的新定义列出不等式组,求出不等式组的解集表示在数轴上即可.
【考点精析】根据题目的已知条件,利用零指数幂法则和整数指数幂的运算性质的相关知识可以得到问题的答案,需要掌握零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数).

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
【题目】为了让同学们了解自己的体育水平,初二1班的体育刘老师对全班45名学生进行了一次体育模拟测试(得分均为整数),成绩满分为10分,1班的体育委员根据这次测试成绩,制作了统计图和分析表如下:
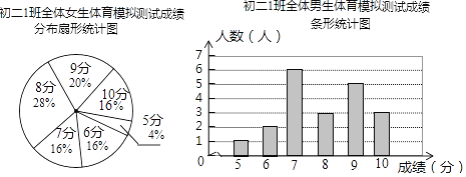
初二1班体育模拟测试成绩分析表
平均分 | 方差 | 中位数 | 众数 | |
男生 | 2 | 8 | 7 | |
女生 | 7.92 | 1.99 | 8 |
根据以上信息,解答下列问题:
(1)这个班共有男生________人,共有女生________人;
(2)补全初二1班体育模拟测试成绩分析表.