Question

【题目】阅读理解：

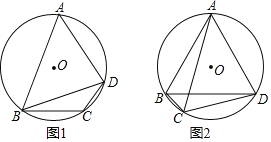
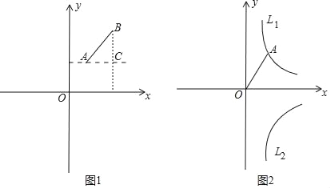
如图（1），在平面直角坐标系xOy中，已知点A的坐标是（1，2），点B的坐标是（3，4），过点A、点B作平行于x轴、y轴的直线相交于点C，得到Rt△ABC，由勾股定理可得，线段AB＝．

得出结论：

（1）若A点的坐标为（x1，y1），B点的坐标为（x2，y2）请你直接用A、B两点的坐标表示A、B两点间的距离；

应用结论：

（2）若点P在y轴上运动，试求当PA＝PB时，点P的坐标．

（3）如图（2）若双曲线L1：y＝（x＞0）经过A（1，2）点，将线段OA绕点O旋转，使点A恰好落在双曲线L2：y＝﹣（x＞0）上的点D处，试求A、D两点间的距离．

Answer 1

【答案】（1）;（2）P（0，5）；(3)

【解析】

（1）根据题目提供的两点间的距离公式即可得出结论；

（2）设出点P，根据题目提供的两点间的距离公式表示出PA，PB，最后利用PA＝PB建立方程求解即可得出结论；

（3）将点A坐标代入双曲线L1的解析式中，求出k，设出点D的坐标，利用题目提供的两点间距离公式表示出OD，再利用旋转得出OA＝OD，建立方程求解，即可得出结论．

解：（1）∵A点的坐标为（x1，y1），B点的坐标为（x2，y2），

∴根据两点间的距离公式得，；

（2）设点P（0，a），

∵A的坐标是（1，2），点B的坐标是（3，4），

∵PA＝，PB＝，

∵PA＝PB，

∴＝，

∴a＝5，

∴P（0，5）；

（3）∵双曲线L1：y＝（x＞0）经过A（1，2）点，

∴OA＝，k＝1×2＝2，

∴双曲线L1：y＝（x＞0），双曲线L2：y＝﹣（x＞0），

设点D坐标为（m，﹣）（m＞0），

∴OD＝，

由旋转知，OA＝OD，

∴＝，

∴m＝±1或m＝±2，

∵m＞0，

∴m＝1（和点A重合，舍去）或m＝2，

∴D（2，﹣1）．

∵A（1，2），

∴AD＝．