题目内容
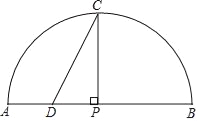
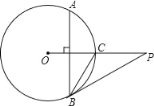
【题目】如图,已知P是⊙O外一点,PO交⊙O于点C,OC=CP=4,弦AB⊥OC,劣弧AB的度数为120°,连接PB.
(1)求BC的长;
(2)求证:PB是⊙O的切线.
【答案】(1)4;(2)详见解析
【解析】
(1)首先连接OB,由弦AB⊥OC,劣弧AB的度数为120°,易证得△OBC是等边三角形,则可求得BC的长;
(2)由OC=CP=4,△OBC是等边三角形,可求得BC=CP,即可得∠P=∠CBP,又由等边三角形的性质,∠OBC=60°,∠CBP =30°,则可证得OB⊥BP,继而证得PB是⊙O的切线.
(1)连接OB,
∵弦AB⊥OC,劣弧AB的度数为120°,
∴弧BC与弧AC的度数为:60°,
∴∠BOC=60°,
∵OB=OC,
∴△OBC是等边三角形,
∴BC=OC=4;
(2)证明:∵OC=CP,BC=OC,
∴BC=CP,
∴∠CBP=∠CPB,
∵△OBC是等边三角形,
∴∠OBC=∠OCB=60°,
∴∠CBP=30°,
∴∠OBP=∠CBP+∠OBC=90°,
∴OB⊥BP,
∵点B在⊙O上,
∴PB是⊙O的切线.

【题目】某商店购进一种商品,每件商品进价30元.试销中发现这种商品每天的销售量y(件)
与每件销售价x(元)的关系数据如下:
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
(1)已知y与x满足一次函数关系,根据上表,求出y与x之间的关系式(不写出自变量x的取值范围);
(2)如果商店销售这种商品,每天要获得150元利润,那么每件商品的销售价应定为多少元?
(3)设该商店每天销售这种商品所获利润为w(元),求出w与x之间的关系式,并求出每件商品销售价定为多少元时利润最大?
【题目】24如图,P是弧AB所对弦AB上一动点,过点P作PC⊥AB交弧AB于点C,取AP中点D,连接CD.已知AB=6cm,设A,P两点间的距离为xcm,C.D两点间的距离为ycm.(当点P与点A重合时,y的值为0;当点P与点B重合时,y的值为3)
小凡根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小凡的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 0 | 2.2 |
| 3.2 | 3.4 | 3.3 | 3 |
(2)建立平面直角坐标系,描出补全后的表中各对对应值为坐标的点,画出该函数的图象;
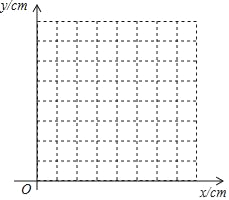
(3)结合所画出的函数图象,解决问题:当∠C=30°时,AP的长度约为 cm.