题目内容
【题目】某公司计划从甲、乙两种产品中选择一种生产并销售,每年产销x件.已知产销两种产品的有关信息如表:
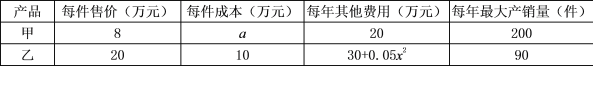
其中a为常数,且5≤a≤7.
(1)若产销甲、乙两种产品的年利润分别为![]() 万元、
万元、![]() 万元,直接写出
万元,直接写出![]() 、
、![]() 与x的函数关系式;(注:年利润=总售价﹣总成本﹣每年其他费用)
与x的函数关系式;(注:年利润=总售价﹣总成本﹣每年其他费用)
(2)分别求出产销两种产品的最大年利润;
(3)为获得最大年利润,该公司应该选择产销哪种产品?请说明理由.
【答案】(1)1)y1=(8-a)x-20,(0<x≤200),![]() =
=![]() (0<x≤90);(2)x=200时,y1的值最大=(1580-200a)万元,当x=90时,
(0<x≤90);(2)x=200时,y1的值最大=(1580-200a)万元,当x=90时,![]() 最大值=465万元;(3)答案见解析
最大值=465万元;(3)答案见解析
【解析】
(1)根据利润=销售数量×每件的利润即可解决问题.
(2)根据一次函数的增减性,二次函数的增减性即可解决问题.
(3)根据题意分三种情形分别求解即可:①(1580-200a)=465,②(1580-200a)>465,③(1580-200a)<465.
(1) 解:(1)y1=(8-a)x-20,(0<x≤200)
![]() =
=![]() .(0<x≤90).
.(0<x≤90).
(2)对于y1=(8-a)x-20.
∵8-a>0,∴x=200时,y1的值最大=(1580-200a)万元.
对于![]() .
.
∵0<x≤90,∴x=90时,![]() 最大值=465万元.
最大值=465万元.
(3)①(1580-200a)=465,解得a=5.575,②(1580-200a)>465,解得a<5.575,③(1580-200a)<465,解得a>5.575.
∵5≤a≤7,∴当a=5.575时,生产甲乙两种产品的利润相同.
当5≤a<5.575时,生产甲产品利润比较高.
当5.575<a≤7时,生产乙产品利润比较高.
(每种情况1分)

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目