题目内容
【题目】如图,四边形ABCD中,∠BAD=∠C=90°,AB=AD,AE⊥BC,垂足为E,若线段AE=3,则四边形ABCD的面积是_____.

【答案】9 .
【解析】
过A点作AF⊥CD交CD的延长线于F点,由AE⊥BC,AF⊥CF,∠C=90°可得四边形AECF为矩形,则∠2+∠3=90°,而∠BAD=90°,根据等角的余角相等得∠1=∠3,加上∠AEB=∠AFD=90°和AB=AD,根据全等三角形的判定可得△ABE≌△ADF,由全等三角形的性质有AE=AF=5,S△ABE=S△ADF,则S四边形ABCD=S正方形AECF,然后根据正方形的面积公式计算即可.
过A点作AF⊥CD交CD的延长线于F点,如图:
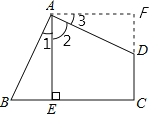
∵AE⊥BC,AF⊥CF,
∴∠AEC=∠CFA=90°,
而∠C=90°,
∴四边形AECF为矩形,
∴∠2+∠3=90°,
又∵∠BAD=90°,
∴∠1=∠3,
在△ABE和△ADF中,
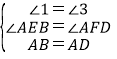
∴△ABE≌△ADF(AAS),
∴AE=AF=3,S△ABE=S△ADF,
∴四边形AECF是边长为3的正方形,
∴S四边形ABCD=S正方形AECF=32=9.
故答案是:9.

【题目】2016年黔西南州教育局组织全州中小学生参加全省安全知识网络竞赛,在全州安全知识竞赛结束后,通过网上查询,某校一名班主任对本班成绩(成绩取整数,满分100分)作了统计分析,绘制成如下频数分布表和频数分布直方图,请你根据图表提供的信息,解答下列问题: 
(1)频数分布表中a= , b= , c=
(2)补全频数分布直方图
(3)为了激励学生增强安全意识,班主任准备从超过90分的学生中选2人介绍学习经验,那么取得100分的小亮和小华同时被选上的概率是多少?请用列表法或画树状图加以说明,并列出所有等可能结果.
频数分布表
分组(分) | 频数 | 频率 |
50<x 60 | 2 | 0.04 |
60<x 70 | 12 | a |
70<x<80 | b | 0.36 |
80<x 90 | 14 | 0.28 |
90<x 100 | c | 0.08 |
合计 | 50 | 1 |






