题目内容
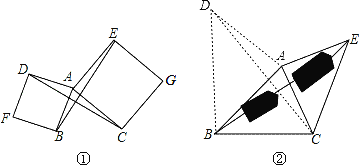
【题目】(1)如图1,已知△ABC,以AB、AC为边分别向外作正方形ABFD和正方形ACGE,连结BE、CD,猜想BE与CD有什么数量关系?并说明理由;
(2)请模仿正方形情景下构造全等三角形的思路,利用构造全等三角形完成下题:如图2,要测量池塘两岸相对的两点B、E的距离,已经测得∠ABC=45°,∠CAE=90°,AB=BC=100米,AC=AE,求BE的长(结果保留根号).

【答案】(1)、CD=BE,证明过程见解析;(2)、100![]() .
.
【解析】
试题分析:(1)、由正方形的性质就可以得出△ADC≌△ABE,就可以得出CD=BE;
(2)、在AB的外侧作AD⊥AB,使AD=AB,连结CD,BD,就可以得出△ADC≌△ABE,就有CD=BE,在Rt△CDB中由勾股定理就可以求出CD的值,进而得出结论.
试题解析:(1)、CD=BE. 理由:如图①∵四边形ABFD和四边形ACGE都是正方形,
∴AD=AB,AC=AE,∠DAB=∠CAE=90°, ∴∠DAB+∠BAC=∠CAE+∠BAC, ∴∠DAC=∠BAE.
在△ADC和△ABE中, 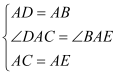 , ∴△ADC≌△ABE(SAS), ∴CD=BE;
, ∴△ADC≌△ABE(SAS), ∴CD=BE;
(2)、如图②,在AB的外侧作AD⊥AB,使AD=AB,连结CD,BD, ∴∠DAB=90°,
∴∠ABD=∠ADB=45°. ∵∠ABC=45°, ∴∠ABD+∠ABC=45°+45°=90°, 即∠DBC=90°.
∴∠CAE=90°, ∴∠DAB=∠CAE, ∴∠DAB+∠BAC=∠CAE+∠BAC, 即∠DAC=∠BAE.
在△ADC和△ABE中 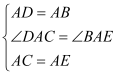 , ∴△ADC≌△ABE(SAS), ∴CD=BE.
, ∴△ADC≌△ABE(SAS), ∴CD=BE.
∵AB=100m,在直角△ABD中,由勾股定理,得 BD=100![]() . ∴CD=
. ∴CD=![]() =100
=100![]() ,
,
∴BE=CD=100![]() ,
,