题目内容
【题目】如图（1），已知A（a，0），B（0，b），且满足a＝
．
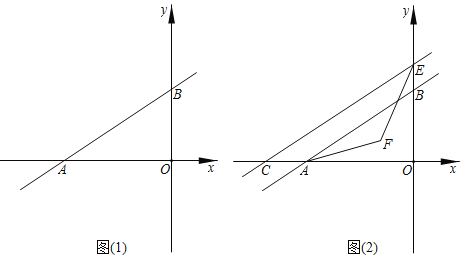
（1）求A、B两点坐标；
（2）在（1）的条件下，Q为直线AB上一点，且满足S△AOQ＝2S△BOQ，求Q点的纵坐标；
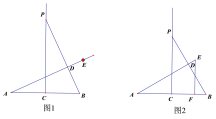
（3）如图（2），E点在y轴上运动，且在B点上方，过E作AB的平行线，交x轴于点C，∠CEO的平分线与∠BAO的平分线交于点F．问：点E在运动过程中，∠F的大小是否发生改变？若改变，请说明理由；若不变，请求出它的值．
【答案】（1）A（﹣6，0），B（0，4）；（2）Q点纵坐标为
或8；（3）∠F的大小不变，∠F＝135°
【解析】
（1）根据二次根式有意义的条件列出不等式，分别求出a、b，得到点A、B两点坐标；
（2）分Q在线段AB上、Q在点B上方、Q在A点下方三种情况，根据三角形的面积公式计算；
（3）根据角平分线的定义、三角形内角和定理、平行线的性质计算，得到答案．
（1）由题意可得：b﹣4≥0，4﹣b≥0，
∴b＝4，
则a＝﹣6，
∴A（﹣6，0），B（0，4）；
（2）∵A（﹣6，0），B（0，4），
∴OA＝6，OB＝4，
∴S△AOB＝
×4×6＝12，
∵Q在直线AB上，
所以点Q位置有3种可能，设点Q到x轴的距离为h，
当Q在线段AB上时，
∵S△AOQ＝2S△BOQ，
∴S△AOQ＝8，S△BOQ＝4，
∴×6×h＝8，
解得，h＝，
∴Q点纵坐标为；
当Q在点B上方时，∵S△AOQ＝2S△BOQ，S△AOQ＝S△AOB+S△BOQ，
∴S△AOB＝S△BOQ，
∴S△AOQ＝24，
∴×6×h＝24，
解得，h＝8，
∴Q点纵坐标为8；
当Q在A点下方时，不符合题意，
综上所述，Q点纵坐标为或8；
（3）∠F的大小不变，
理由如下：∵AB∥CE，
∴∠BAO＝∠ECO，∠ADF＝∠CEF，
∵∠EOC＝90°，
∴∠ECO+∠CEO＝90°，
∵AF平分∠BAO，EF平分∠CEO，
∴∠DAF＝∠BAO，∠CEF＝∠CEO，
∴∠DAF＝∠ECO，∠ADF＝∠CEO
∴∠DAF+∠ADF＝∠ECO+ ∠CEO
＝（∠ECO+∠CEO）
＝×90°
＝45°，
∴∠F＝180°﹣（∠DAF+∠ADF）
＝180°﹣45°
＝135°．
