题目内容
【题目】在等腰△ABC中,AB=AC,则有BC边上的中线,高线和∠BAC的平分线重合于AD(如图一).若将等腰△ABC的顶点A向右平行移动后,得到△A′BC(如图二),那么,此时BC边上的中线、BC边上的高线和∠BA′C的平分线应依次分别是 , , .(填A′D、A′E、A′F)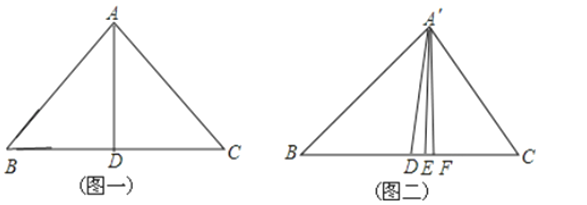
【答案】A′D;AF;AE
【解析】解:
在等腰△ABC中,AB=AC,则有BC边上的中线,高线和∠BAC的平分线重合于AD(如图一).若将等腰△ABC的顶点A向右平行移动后,得到△A′BC(如图二),那么,此时BC边上的中线、BC边上的高线和∠BA′C的平分线应依次分别是 A′D,AF,AE,
所以答案是:A′D,A′F,A′E.
【考点精析】掌握平移的性质是解答本题的根本,需要知道①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等.

练习册系列答案
相关题目

