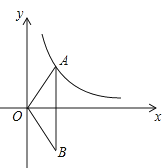题目内容
【题目】已知实数a , b满足a-b=1,a2-ab+2>0,当1≤x≤2时,函数y= ![]() (a≠0)的最大值与最小值之差是1,求a的值
(a≠0)的最大值与最小值之差是1,求a的值
【答案】解答:∵a2-ab+2>0,
∴a2-ab>-2,
a(a-b)>-2,
∵a-b=1,
∴a>-2,
① -2<a<0,1≤x≤2时,函数y= ![]() 的最大值是y=
的最大值是y= ![]() ,最小值是y=a ,
,最小值是y=a ,
∵最大值与最小值之差是1,
∴ ![]() -a=1,
-a=1,
解得:a=-2,不合题意,舍去;
②当a>0,1≤x≤2时,函数y= ![]() 的最大值是y=a , 最小值是y=
的最大值是y=a , 最小值是y= ![]() ∵最大值与最小值之差是1,
∵最大值与最小值之差是1,
∴a- ![]() =1,
=1,
解得:a=2,符合题意,
∴a的值是2.
【解析】首先根据条件a-b=1,a2-ab+2>0可确定a>-2,然后再分情况进行讨论:①当-2<a<0,1≤x≤2时,函数y= ![]() 的最大值是y=
的最大值是y= ![]() ,最小值是y=a , ②当a>0,1≤x≤2时,函数y=
,最小值是y=a , ②当a>0,1≤x≤2时,函数y= ![]() 的最大值是y=a , 最小值是y=
的最大值是y=a , 最小值是y= ![]() ,再分别根据最大值与最小值之差是1,计算出a的值
,再分别根据最大值与最小值之差是1,计算出a的值
【考点精析】根据题目的已知条件,利用反比例函数的图象和反比例函数的性质的相关知识可以得到问题的答案,需要掌握反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点;性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.

练习册系列答案
相关题目