题目内容
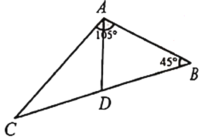
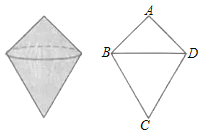
【题目】如图物体由两个圆锥组成．其主视图中，
，
，若上面圆锥的侧面积为
，则下面圆锥的侧面积为（ ）
A.2B.
C.
D.
【答案】A
【解析】
先证明△ABD为等腰直角三角形得到∠ABD=45°，BD=
AB，再证明△CBD为等边三角形得到BC=BD=AB，利用圆锥的侧面积的计算方法得到上面圆锥的侧面积与下面圆锥的侧面积的比等于AB：CB，从而得到下面圆锥的侧面积．
解：∵∠A=90°，AB=AD，
∴△ABD为等腰直角三角形，
∴∠ABD=45°，BD=AB，
∵∠ABC=105°，
∴∠CBD=60°，
而CB=CD，
∴△CBD为等边三角形，
∴BC=BD=AB，
∵上面圆锥与下面圆锥的底面相同，
∴上面圆锥的侧面积与下面圆锥的侧面积的比等于AB：CB，
∴下面圆锥的侧面积=
．
故选：A．
【题目】某校学生会准备调查七年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数．
类别 | 频数（人数） | 频率 |
武术类 | 0.20 | |
书画类 | 15 | 0.l5 |
棋牌类 | 25 |
|
器乐类 | ||
合计 |
| 1.00 |
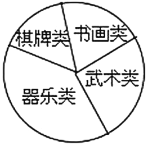
（1）确定调查方式时，甲同学说：“我到七年级（1）班去调查全体同学”；乙同学说：“放学时我到校门口随机调查部分同学”；丙同学说：“我到七年级每个班随机调查一定数量的同学”．请指出哪位同学的调查方式最合理．
（2）他们采用了最为合理的调查方法收集数据，并绘制了如图所示的统计表和扇形统计图.请你根据以上图表提供的信息解答下列问题：
①
____，
_____；
②在扇形统计图中，器乐类所对应扇形的圆心角是_____度；
③若该校七年级有学生460人，请你估计大约有多少学生参加武术类校本课程．
【题目】今年疫情防控期间，我市一家服装有限公司生产了一款服装，为对比分析以前实体商店和现在网上商店两种途径的销售情况，进行了为期30天的跟踪调查．其中实体商店的日销售量
（百件）与时间
（为整数，单位：天）的部分对应值如下表所示；网上商店的日销售量
（百件）与时间（为整数，单位：天）的关系如图所示．
时间 | 0 | 6 | 10 | 12 | 18 | 20 | 24 | 30 |
日销售量 | 0 | 72 | 100 | 108 | 108 | 100 | 72 | 0 |
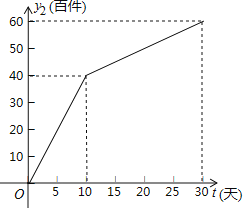
（1）请你在一次函数、二次函数和反比例函数中，选择合适的函数反映与的变化规律，并求出与的函数关系式及自变量的取值范围；
（2）求与的函数关系式，并写出自变量的取值范围；
（3）在跟踪调查的30天中，设实体商店和网上商店的日销售总量为
（百件），求与的函数关系式；当为何值时，日销售量达到最大，并求出此时的最大值．
