Question

【题目】为践行“绿水青山就是金山银山”的重要思想，某森林保护区开展了寻找古树活动，如图，在一个坡度(坡比)的山坡上发现一棵古树，测得古树低端到山脚点的距离米，在距山脚点水平距离米的点处，测得古树顶端的仰角(古树与山坡的剖面、点在同一平面内，古树与直线垂直)，求古树的高度约为多少米？ (结果保留一位小数，参考数据)

Answer 1

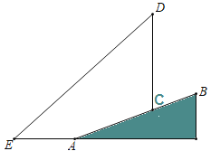
【答案】23.3米

【解析】

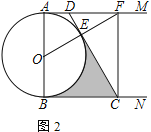
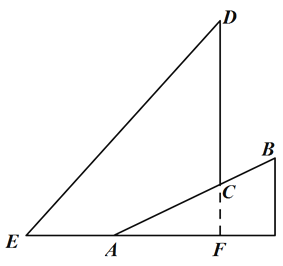
延长DC交EA的延长线于点F，则CF⊥EF，设CF＝k，由i＝1:2.4，则AF＝2.4k，在Rt△ACF中，根据勾股定理得到列方程求k值，从而求得CF的长，然后在Rt△DEF中，利用tanE＝解直角三角形求得DF的长，从而使问题得解．

解：延长交直线于点，则 ，

∴设CF＝k，由i＝1:2.4，则AF＝2.4k，

在Rt△ACF中，由勾股定理得，

∴，

解得：k＝10，

∴CF＝10，AF＝24，

∴EF＝AF＋AE＝30．

在Rt△DEF中，tanE＝

∴

故古树的高度约为米．