题目内容
【题目】如图,AB是⊙O的直径,点P是弦BC上一动点(不与B,C重合),过点P作PE⊥AB,垂足为E,在射线EP上取点D使得DC=DP,连接DC.
(1)求证:DC是⊙O的切线;
(2)若∠CBA=30°,射线EP交⊙O于点 F,当点 F恰好是弧BC的中点时,判断以B,O,C,F为顶点的四边形是什么特殊四边形?说明理由.
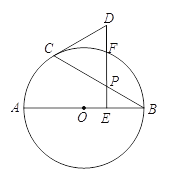
【答案】(1)证明见解析;(2)四边形BOCF为菱形,理由见解析.
【解析】(1)证明:连接OC,
∵DP=DC,∴∠DPC=∠DCP,∵∠DPC=∠BPE,∴∠BPE=∠DCP,
∵PE⊥AB,∴∠BEP=90°,∴∠B+∠APE=90°,
∵OB=OC,∴∠OCB=∠B,∴∠OCB+∠DCP=90°,
∴OC⊥CD, ∴直线CD与⊙O相切;
(2)解:以B、O、C、F为顶点的四边形是菱形,
连接AC,∵∠CBA=30°,∴∠A=60°,
∴△OAC为等边三角形,∴∠BOC=120°,
连接OF,BF,CF
∵F是弧BC的中点,∴∠BOF=∠COF=60°,
∴△BOF与△COF均为等边三角形,
∴BF=BO=OC=CF,∴四边形BOCF为菱形.

练习册系列答案
相关题目
【题目】某学习小组13名学生的一次英语听力测试成绩分布如下表所示(满分20分):
成绩(分) | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
人数(人) | 1 | 3 | 2 | 2 | 1 | 2 | 2 |
这13名学生听力测试成绩的中位数是( )
A.16分
B.17分
C.18分
D.19分
