Question

【题目】如图，抛物线与轴交于，两点，与轴交于点，顶点为，以为直径作D．下列结论：①抛物线的对称轴是直线x=3；②⊙D的面积为16π；③抛物线上存在点E，使四边形ACED为平行四边形；④直线CM与⊙D相切．其中正确结论的个数是（　　）

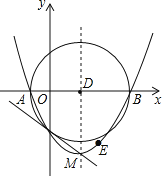
A. 1 B. 2 C. 3 D. 4

Answer 1

【答案】B

【解析】

①根据抛物线的解析式得出抛物线与x轴的交点A、B坐标，由抛物线的对称性即可判定；②求得⊙D的直径AB的长，得出其半径，由圆的面积公式即可判定，③过点C作CE∥AB，交抛物线于E，如果CE=AD，则根据一组对边平行且相等的四边形是平行四边形即可判定；④求得直线CM、直线CD的解析式通过它们的斜率进行判定．

∵在y=（x+2）（x-8）中，当y=0时，x=-2或x=8，

∴点A（-2，0）、B（8，0），

∴抛物线的对称轴为x==3，故①正确；

∵⊙D的直径为8-（-2）=10，即半径为5，

∴⊙D的面积为25π，故②错误；

在y=（x+2）（x-8）=x2-x-4中，当x=0时y=-4，

∴点C（0，-4），

当y=-4时，x2-x-4=-4，

解得：x1=0、x2=6，

所以点E（6，-4），

则CE=6，

∵AD=3-（-2）=5，

∴AD≠CE，

∴四边形ACED不是平行四边形，故③错误；

∵y=x2-x-4=（x-3）2-，

∴点M（3，-），

设直线CM解析式为y=kx+b，

将点C（0，-4）、M（3，-）代入，

得：，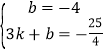

解得：，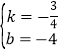

所以直线CM解析式为y=-x-4；

设直线CD解析式为y=mx+n，

将点C（0，-4）、D（3，0）代入，得：，

解得：，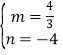

所以直线CD解析式为y=x-4，

由-×=-1知CM⊥CD于点C，

∴直线CM与⊙D相切，故④正确；

故选：B．