Question

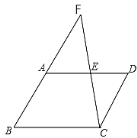
【题目】如图，四边形ABCD是平行四边形，∠B=60°，点E是AD的中点，CE的延长线与BA的延长线相交于点F，BC=2.

(1)求证:△AFE≌△DCE；

(2)连接AC、DF，填空：

①当AB=_______时，以A、C、D、F为顶点的四边形是矩形；

②当AB=_______时，以A、C、D、F为顶点的四边形是菱形。

Answer 1

【答案】（1）详见解析；（2）1；2.

【解析】

（1）依据“ASA”证明△AFE≌△DCE即可；

（2）分别根据矩形和菱形的性质求解即可.

（1）证明：∵四边形ABCD是平行四边形，

∴AB=DC，AB∥DC，

∴∠FAE=∠D，∠F=∠ECD，

又∵EA=ED，

∴△AFE≌△DCE，

（2）∵四边形ABCD是平行四边形，

∴AB∥CD，AB=CD，AD∥BC，AD=BC，

∵∠B=60°，

∴∠D=60°.

①若四边形ACDF为矩形，则有∠ACD=90°，

∴∠CAD=30°，

∴CD=AD=BC=，

即当AB=1时，以A、C、D、F为顶点的四边形是矩形；

②若四边形ACDF为菱形，则有AC=CD=DF=FA，

∵∠D=∠B=60°

∴△ACD为等边三角形，

∴CD=AD=2，

即当AB=2时，以A、C、D、F为顶点的四边形是菱形.