题目内容
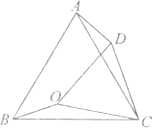
【题目】如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于![]() BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=58°,则∠ABC的度数为( )
BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=58°,则∠ABC的度数为( )
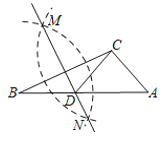
A. 29°B. 30°C. 31°D. 32°
【答案】A
【解析】
依次连接CM、MB、BN、NC,则四边形CMBN为菱形,由此得出:∠BND=∠CND,根据全等三角形的判定定理,证明![]() BND≌△CND,则BD=CD,故:△BDC是等腰三角形.CD=AC且∠A=58°,则∠CDA=58°,根据外角性质得出结果.
BND≌△CND,则BD=CD,故:△BDC是等腰三角形.CD=AC且∠A=58°,则∠CDA=58°,根据外角性质得出结果.
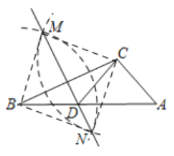
依次连接CM、MB、BN、NC,则四边形CMBN为菱形,
则∠BND=∠CND.
在△BND和△CND中,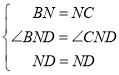 ,
,
△BND≌△CND,
则BD=CD,
∴△BDC是等腰三角形,
∠ABC=∠DCB,
在△ACD中,CD=AC且∠A=58°,则∠CDA=58°,
由三角形外角性质:∠CDA=∠ABC+∠DCB=2∠ABC,
即58°=2∠ABC,
则∠ABC=29°

练习册系列答案
相关题目