题目内容
梯形ABCD中，AB∥DC，CD=8，AB=12，S四边形ABCD=90，两腰的延长线相交于点M，则S△MCD=________．
72
分析：首先根据题意画出图形，然后由AB∥DC，可得△ABM∽△DCM，又由相似三角形的面积比等于相似比的平方，求得答案．
解答：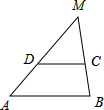
解：∵AB∥DC，
∴△ABM∽△DCM，
∴
=（
）2，
∵CD=8，AB=12，S四边形ABCD=90，
∴
=（
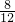）2，
解得：S△MCD=72．
故答案为：72．
点评：此题考查了相似三角形的判定与性质．此题比较简单，注意掌握数形结合思想与方程思想的应用．
分析：首先根据题意画出图形，然后由AB∥DC，可得△ABM∽△DCM，又由相似三角形的面积比等于相似比的平方，求得答案．
解答：
解：∵AB∥DC，∴△ABM∽△DCM，
∴
=（）2，∵CD=8，AB=12，S四边形ABCD=90，
∴
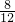=（）2，解得：S△MCD=72．
故答案为：72．
点评：此题考查了相似三角形的判定与性质．此题比较简单，注意掌握数形结合思想与方程思想的应用．
练习册系列答案
智能训练练测考系列答案
相关题目
如图，已知在等腰梯形ABCD中，AB∥CD，AB＜CD，AB=10，BC=3．
如图，等腰梯形ABCD中，AB∥DC，∠A=60°，AD=DC=10，点E，F分别在AD，BC上，且AE=4，BF=x，设四边形DEFC的面积为y，则y关于x的函数关系式是
5、如图，等腰梯形ABCD中，AB∥DC，AD=AB=BC=6，且∠D=60°，则DC=（ ）
如图，已知梯形ABCD中，AB∥CD，∠ABC=90°，CD=1．