题目内容
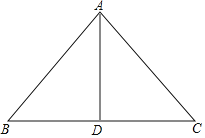
【题目】问题原型:如图①,在锐角△ABC中,∠ABC=45°,AD⊥BC于点D,在AD上取点E,使DE=CD,连结BE.求证:BE=AC.
问题拓展:如图②,在问题原型的条件下,F为BC的中点,连结EF并延长至点M,使FM=EF,连结CM.
(1)判断线段AC与CM的大小关系,并说明理由.
(2)若AC=![]() ,直接写出A、M两点之间的距离.
,直接写出A、M两点之间的距离.

【答案】问题原型:见解析; 问题拓展:(1)AC=CM,理由见解析;(2)AM=![]() .
.
【解析】
根据题意证出△BDE≌△ADC即可得出答案;
证出△BEF≌△CMF即可得出答案;
(2)连接AM,求出∠ACM=90°,即可求出A
问题原型:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∵∠ABC=45°,
∴∠BAD=45°,
∴∠ABC=∠BAD,
∴AD=BD,
在△BDE和△ADC中,
∵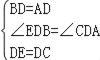 ,
,
∴△BDE≌△ADC(SAS),
∴BE=AC,
问题拓展:(1)AC=CM,理由:
∵点F是BC中点,
∴BF=CF,
在△BEF和△CMF中,
∵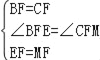 ,
,
∴△BEF≌△CMF(SAS),
∴BE=CM,
由(1)知,BE=AC,
∴AC=CM;
(2)如图②,
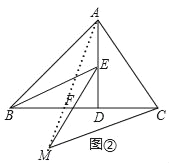
连接AM,由(1)知,△BDE≌△ADC,
∴∠BED=∠ACD,
由(2)知,△BEF≌△CMF,
∴∠EBF=∠BCM,
∴∠ACM=∠ACD+∠BCM=∠BED+∠EBF=90°,
∵AC=CM,
∴AM=![]() AC=
AC=![]() .
.

练习册系列答案
相关题目