题目内容
【题目】为了迎接全市体育中考,某中学对全校初三男生进行了立定跳远项目测试,并从参加测试的![]() 名男生中随机抽取了部分男生的测试成绩(单位:米,精确到
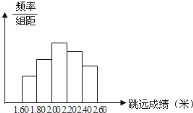
名男生中随机抽取了部分男生的测试成绩(单位:米,精确到![]() 米)作为样本进行分析,绘制了如图所示的频率分布直方图(每组含最低值,不含最高值).已知图中从左到右每个小长方形的高的比依次为
米)作为样本进行分析,绘制了如图所示的频率分布直方图(每组含最低值,不含最高值).已知图中从左到右每个小长方形的高的比依次为![]() ,其中
,其中![]() 的频数为
的频数为![]() ,请根据有关信息解答下列问题:
,请根据有关信息解答下列问题:
![]() 填空:这次调查的样本容量为________,
填空:这次调查的样本容量为________,![]() 这一小组的频率为________;
这一小组的频率为________;
![]() 请指出样本成绩的中位数落在哪一小组内,并说明理由;
请指出样本成绩的中位数落在哪一小组内,并说明理由;
![]() 样本中男生立定跳远的人均成绩不低于多少米;
样本中男生立定跳远的人均成绩不低于多少米;
![]() 请估计该校初三男生立定跳远成绩在
请估计该校初三男生立定跳远成绩在![]() 米以上(包括
米以上(包括![]() 米)的约有多少人?
米)的约有多少人?
【答案】(1)![]() ;(2)中位数落在
;(2)中位数落在![]() 这一小组内;(3)样本中男生立定跳远的人均成绩不低于
这一小组内;(3)样本中男生立定跳远的人均成绩不低于![]() 米;(4)该校初三男生立定跳远成绩在
米;(4)该校初三男生立定跳远成绩在![]() 米以上的约有
米以上的约有![]() 人.
人.
【解析】
(1)每小组的频率=小组的频数÷总人数.第2小组的频数为8;这5个小组频率之比为2:4:6:5:3,可求得第2组频率为0.2;即可求的样本容量即总人数;
(2)根据中位数的求法,将数据从小到大排列,找最中间两个数的平均数即可得出答案;
(3)计算其平均数即可得答案;
(4)用样本估计总体.
(1)样本容量=(2+4+6+5+3)÷4×8=40;![]() =3÷20=0.15;
=3÷20=0.15;
![]() ∵各小组的频数分别为:
∵各小组的频数分别为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
而中位数是![]() 个成绩从小到大排列后第
个成绩从小到大排列后第![]() 个数据和第
个数据和第![]() 个数据的平均数,
个数据的平均数,
∴中位数落在![]() 这一小组内;
这一小组内;
![]() 设样本人均成绩最低值为
设样本人均成绩最低值为![]() ,
,
则![]() ,
,
∴样本中男生立定跳远的人均成绩不低于![]() 米;
米;
![]() 估计该校初三男生立定跳远成绩在
估计该校初三男生立定跳远成绩在![]() 米以上(包括
米以上(包括![]() 米)的约有
米)的约有![]() (人))
(人))
所以该校初三男生立定跳远成绩在![]() 米以上的约有
米以上的约有![]() 人.
人.

练习册系列答案
相关题目