题目内容
如图，直线l1：
与双曲线
相交于点A（a，2），将直线l1向上平移3个单位得到l2，直线l2与双曲线相交于B．C两点（点B在第一象限），交y轴于D点．
（1）求双曲线的解析式；
（2）求tan∠DOB的值．
与双曲线相交于点A（a，2），将直线l1向上平移3个单位得到l2，直线l2与双曲线相交于B．C两点（点B在第一象限），交y轴于D点．（1）求双曲线
的解析式；（2）求tan∠DOB的值．
（1）
（2）
（2）解：（1）∵A（a，2）是y=x与的交点，∴A（2，2）。
把A（2，2）代入，得k=4。
∴双曲线的解析式为。
（2）∵将l1向上平移了3个单位得到l2，∴l2的解析式为y=x+3。
∴解方程组
，得
。
∴B （1，4）。∴tan∠DOB=。
（1）由点A（a，2）在直线y=x上可知a=2，再代入 中求k的值即可得。
（2）将l1向上平移了3个单位得到l2的解析式为y=x+3，联立l2与双曲线解析式求交点B坐标，根据B点坐标，利用锐角三角函数定义求解。
的交点，∴A（2，2）。把A（2，2）代入
，得k=4。∴双曲线的解析式为
。（2）∵将l1向上平移了3个单位得到l2，∴l2的解析式为y=x+3。
∴解方程组
，得。∴B （1，4）。∴tan∠DOB=
。（1）由点A（a，2）在直线y=x上可知a=2，再代入
中求k的值即可得。（2）将l1向上平移了3个单位得到l2的解析式为y=x+3，联立l2与双曲线解析式求交点B坐标，根据B点坐标，利用锐角三角函数定义求解。
练习册系列答案
相关题目
图象过第二象限内的点A（—2，m）AB⊥x轴于B，Rt△AOB面积为3, 若直线y=ax+b经过点A，并且经过反比例函数
分别表示A艇和B艇，相对于海岸的距离y（海里）与追赶时间x（分钟）之间的一次函数的关系 （15分）
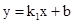的图象过点A(0,3)，且与反比例函数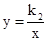
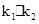的值；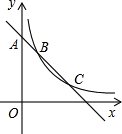
.在x轴上取一点P，过点P作直线OA的垂线l，以直线l为对称轴，线段OB经轴对称变换后的像是O´B´.当点O´与点A重合时，点P的坐标是 ；
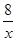的上的两个点，若x2＞x1＞0，则（ ）
的图象经过点（3，－4），则此函数在每一个象限内
随
的增大而 ．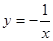
与正比例函数
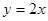在同一坐标系内的大致图像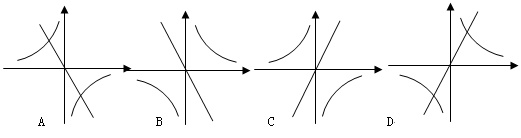为（ ）.
的图象上，则a的值为（ ）