题目内容
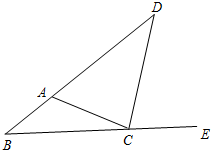 如图:CD是△ABC中∠ACB的外角平分线,请猜测∠BAC和∠B的大小关系,并说明理由.
如图:CD是△ABC中∠ACB的外角平分线,请猜测∠BAC和∠B的大小关系,并说明理由.分析:根据角平分线的定义可得∠ACD=∠ECD,然后根据三角形的一个外角大于任何一个与它不相邻的内角可得∠BAC>∠ACD,∠ECD>∠B,从而得解.
解答:解:∠BAC>∠B.
理由如下:∵CD是△ABC中∠ACB的外角平分线,
∴∠ACD=∠ECD,
∵∠BAC是△ACD的外角,
∴∠BAC>∠ACD,
∴∠BAC>∠ECD,
∵∠ECD是△BCD的外角,
∴∠ECD>∠B,
∴∠BAC>∠B.
理由如下:∵CD是△ABC中∠ACB的外角平分线,
∴∠ACD=∠ECD,
∵∠BAC是△ACD的外角,
∴∠BAC>∠ACD,
∴∠BAC>∠ECD,
∵∠ECD是△BCD的外角,
∴∠ECD>∠B,
∴∠BAC>∠B.
点评:本题考查了三角形的任意两边之和大于第三边的性质,熟记性质并准确识图是解题的关键.

练习册系列答案
相关题目
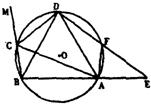 26、已知:如图,CD是△ABC外角∠MCA的平分线,CD与三角形的外接圆交于点D.
26、已知:如图,CD是△ABC外角∠MCA的平分线,CD与三角形的外接圆交于点D.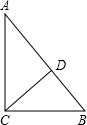 已知:如图,CD是△ABC的高,AC=4,BC=3,DB=
已知:如图,CD是△ABC的高,AC=4,BC=3,DB=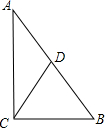 如图,CD是△ABC的中线,且CD=
如图,CD是△ABC的中线,且CD=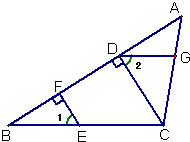 25、如图,CD是△ABC的高,点E、F、G分别在BC、AB、AC上,且EF⊥AB,DG∥BC.试判断∠1、∠2的数量关系,并说明理由.
25、如图,CD是△ABC的高,点E、F、G分别在BC、AB、AC上,且EF⊥AB,DG∥BC.试判断∠1、∠2的数量关系,并说明理由. 如图,CD是△ABC的高,点E、F、G分别在BC、AB、AC上,且EF⊥AB,DG∥BC.试判断∠1、∠2的数量关系,并说明理由.
如图,CD是△ABC的高,点E、F、G分别在BC、AB、AC上,且EF⊥AB,DG∥BC.试判断∠1、∠2的数量关系,并说明理由.