题目内容
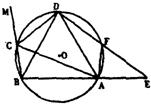 26、已知:如图,CD是△ABC外角∠MCA的平分线,CD与三角形的外接圆交于点D.
26、已知:如图,CD是△ABC外角∠MCA的平分线,CD与三角形的外接圆交于点D.(1)若∠BCA=60°,求证:△ABD为等边三角形;
(2)设点F为弧AD上一点,且弧AF=弧BC,DF的延长线BA的延长线点E.
求证:AC•AF=DF•FE.
分析:(1)可通过证三个内角都是60°来得出三角形ABD是等边三角形的结论.已知∠BCA=60°,根据圆周角定理我们可得出∠BDA=60°,那么我们只需证明∠DBA=∠DAB即可得出三角形是等边三角形的结论.可通过寻找相等的中间值来求解,∠MCD是圆内角四边形ABCD的外角,那么∠MCD=∠DAB,而根据圆周角定理,我们知道∠DBA=∠DCA,已知了DC平分∠MCA,那么我们就可以得出∠DBA=∠DAB的结论,也就能得出本题要求的结论.
(2)可通过相似三角形来求解,可通过证三角形ACD和AFE相似,得出关于AC,CD,AF,FE然后通过证明三角形BCD和三角形AFD全等,得出DF=DC,然后将比例关系式总的等量线段置换,即可得出本题的结果.
(2)可通过相似三角形来求解,可通过证三角形ACD和AFE相似,得出关于AC,CD,AF,FE然后通过证明三角形BCD和三角形AFD全等,得出DF=DC,然后将比例关系式总的等量线段置换,即可得出本题的结果.
解答:证明:(1)∵CD平分∠MCA,
∴∠MCD=∠DCA.
∵∠MCD是圆内接四边形ABCD的外角,
∴∠MCD=∠DAB.
根据圆周角定理可知
∠BDA=∠BCA=60°,∠DCA=∠DBA,
∴∠MCD=∠DCA=∠BDA=∠DBA=∠DAB=60°.
∴△ABD是等边三角形.
(2)由(1)可知∠MCD=∠DCA=60°,
同理可得出∠EFA=∠DBA=60°,
∴∠DCB=∠DFA=180-60=120°.
∵弧BC=弧AF,
∴AF=BC,∠BDC=∠ADF.
∴△BDC≌△ADF.
∴AF=BC.
∵∠EFA=∠DBA=60°,∠DCA=∠DBA=60°,
∴∠EFA=∠DBA.
∵∠BDC=∠ADF,
∴∠BDC+∠ADB=∠ADF+∠ADB,即∠CDA=∠BDF.
∵∠EAF是圆内接三边形ABDF的外角,
∴∠EAF=∠ADF=∠CDA.
∴△ADC∽△EFA.
∴AC•AF=CD•FE.
∵CD=DF,
∴AC•AF=DF•FE.
∴∠MCD=∠DCA.
∵∠MCD是圆内接四边形ABCD的外角,
∴∠MCD=∠DAB.
根据圆周角定理可知
∠BDA=∠BCA=60°,∠DCA=∠DBA,
∴∠MCD=∠DCA=∠BDA=∠DBA=∠DAB=60°.
∴△ABD是等边三角形.
(2)由(1)可知∠MCD=∠DCA=60°,
同理可得出∠EFA=∠DBA=60°,
∴∠DCB=∠DFA=180-60=120°.
∵弧BC=弧AF,
∴AF=BC,∠BDC=∠ADF.
∴△BDC≌△ADF.
∴AF=BC.
∵∠EFA=∠DBA=60°,∠DCA=∠DBA=60°,
∴∠EFA=∠DBA.
∵∠BDC=∠ADF,
∴∠BDC+∠ADB=∠ADF+∠ADB,即∠CDA=∠BDF.
∵∠EAF是圆内接三边形ABDF的外角,
∴∠EAF=∠ADF=∠CDA.
∴△ADC∽△EFA.
∴AC•AF=CD•FE.
∵CD=DF,
∴AC•AF=DF•FE.
点评:(1)本题主要考查了相似三角形的判定和性质,全等三角形的判定和性质,等边三角形的性质以及圆周角定理等知识点,(2)题中准确找出与所求线段相关的相似三角形是解题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
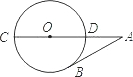 已知:如图,CD是⊙O的直径,点A在CD的延长线上,AB切⊙O于点B,若∠A=30°,OA=10,则AB=
已知:如图,CD是⊙O的直径,点A在CD的延长线上,AB切⊙O于点B,若∠A=30°,OA=10,则AB=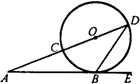 1、已知:如图,CD是⊙O的直径,AE切⊙O于点B,DC的延长线交AB于点A,∠A=20°,则∠DBE=
1、已知:如图,CD是⊙O的直径,AE切⊙O于点B,DC的延长线交AB于点A,∠A=20°,则∠DBE=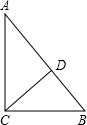 已知:如图,CD是△ABC的高,AC=4,BC=3,DB=
已知:如图,CD是△ABC的高,AC=4,BC=3,DB=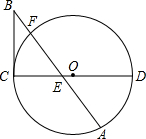 (2006•河北区一模)已知,如图,CD是⊙O的直径,BC是⊙O的切线,切点为C,BC=
(2006•河北区一模)已知,如图,CD是⊙O的直径,BC是⊙O的切线,切点为C,BC=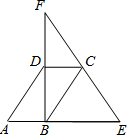 已知,如图,CD是Rt△FBE的中位线,A是EB延长线上一点,AD∥BC.
已知,如图,CD是Rt△FBE的中位线,A是EB延长线上一点,AD∥BC.