题目内容
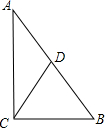 如图,CD是△ABC的中线,且CD=
如图,CD是△ABC的中线,且CD=| 1 | 2 |
分析:根据“CD是△ABC的中线,且CD=
AB”求出AD=CD,BD=CD,再根据三角形内角和定理可得∠ACD+∠BCD=90°,即∠ACB是90°.
| 1 |
| 2 |
解答:解:∵CD是△ABC的中线,且CD=
AB,
∴AD=CD,BD=CD,
∴∠A=∠ACD,∠B=∠BCD
又∵∠A+∠ACD+∠B+∠BCD=180°,
∴∠ACD+∠BCD=90°,
即∠ACB=90°.
由此可得,如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.
| 1 |
| 2 |
∴AD=CD,BD=CD,
∴∠A=∠ACD,∠B=∠BCD
又∵∠A+∠ACD+∠B+∠BCD=180°,
∴∠ACD+∠BCD=90°,
即∠ACB=90°.
由此可得,如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.
点评:本题主要利用中线定义和等边对等角的性质.

练习册系列答案
相关题目
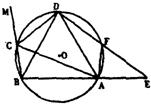 26、已知:如图,CD是△ABC外角∠MCA的平分线,CD与三角形的外接圆交于点D.
26、已知:如图,CD是△ABC外角∠MCA的平分线,CD与三角形的外接圆交于点D.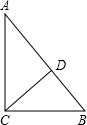 已知:如图,CD是△ABC的高,AC=4,BC=3,DB=
已知:如图,CD是△ABC的高,AC=4,BC=3,DB=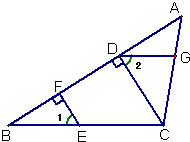 25、如图,CD是△ABC的高,点E、F、G分别在BC、AB、AC上,且EF⊥AB,DG∥BC.试判断∠1、∠2的数量关系,并说明理由.
25、如图,CD是△ABC的高,点E、F、G分别在BC、AB、AC上,且EF⊥AB,DG∥BC.试判断∠1、∠2的数量关系,并说明理由. 如图,CD是△ABC的高,点E、F、G分别在BC、AB、AC上,且EF⊥AB,DG∥BC.试判断∠1、∠2的数量关系,并说明理由.
如图,CD是△ABC的高,点E、F、G分别在BC、AB、AC上,且EF⊥AB,DG∥BC.试判断∠1、∠2的数量关系,并说明理由.