题目内容
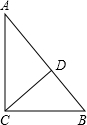已知：如图，CD是△ABC的高，AC=4，BC=3，DB=| 9 | 5 |
（1）求AD的长；
（2）△ABC是直角三角形吗？请说明理由．
分析：①在Rt△BDC中已知两边长可以求出CD的长，在直角三角形ACD中也是已知两边长利用可以求出AD的长．
②利用勾股定理的逆定理，AB2=AC2+BC2是否成立，若成立则是直角三角形，反之不是．
②利用勾股定理的逆定理，AB2=AC2+BC2是否成立，若成立则是直角三角形，反之不是．
解答：解：①在直角三角形BDC中
BC=3，BD=
．
∴CD=
=
．
∴在直角三角形ADC中
AD=
=
．
②由①得AB=AD+BD=
+
=5．
∴在三角形ACB中
AB2=25，AC2+BC2=16+9=25．
∴AB2=AC2+BC2．
∴三角形ACB是直角三角形．
BC=3，BD=
| 9 |
| 5 |
∴CD=
| BC2-BD2 |
| 12 |
| 5 |
∴在直角三角形ADC中
AD=
| AC2-CD2 |
| 16 |
| 5 |
②由①得AB=AD+BD=
| 16 |
| 5 |
| 9 |
| 5 |
∴在三角形ACB中
AB2=25，AC2+BC2=16+9=25．
∴AB2=AC2+BC2．
∴三角形ACB是直角三角形．
点评：①利用勾股定理已知两边求第三边的长．
②利用勾股定理的逆定理判断三角形的形状．
②利用勾股定理的逆定理判断三角形的形状．
练习册系列答案
相关题目
已知：如图，CD是⊙O的直径，点A在CD的延长线上，AB切⊙O于点B，若∠A=30°，OA=10，则AB=
1、已知：如图，CD是⊙O的直径，AE切⊙O于点B，DC的延长线交AB于点A，∠A=20°，则∠DBE=
（2006•河北区一模）已知，如图，CD是⊙O的直径，BC是⊙O的切线，切点为C，BC=
已知，如图，CD是Rt△FBE的中位线，A是EB延长线上一点，AD∥BC．