��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��B������ֱ��ǣ���3��0������0��6��������P�ӵ�O��������x����������ÿ��1����λ���ٶ��˶���ͬʱ����C�ӵ�B������������BO������ÿ��2����λ���ٶ��˶�����CP��COΪ�ڱ߹���PCOD�����߶�OP�ӳ�����ȡ��E��ʹPE=AO�����P�˶���ʱ��Ϊt�룮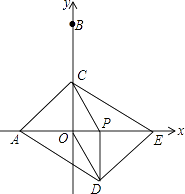
��1������C�˶����߶�OB���е�ʱ����t��ֵ����E�����ꣻ
��2������C���߶�OB��ʱ����֤���ı���ADECΪƽ���ı��Σ�
��3�����߶�PE��ȡ��F��ʹPF=2������F��MN��PE����ȡFM= ![]() ��FN=1���ҵ�M��N�ֱ��ڵ�һ�������ޣ����˶������У�����M��N�У���һ�������ı���ADEC�ı���ʱ��ֱ��д����������������t��ֵ��
��FN=1���ҵ�M��N�ֱ��ڵ�һ�������ޣ����˶������У�����M��N�У���һ�������ı���ADEC�ı���ʱ��ֱ��д����������������t��ֵ��
���𰸡�
��1��
�⣺BC= ![]() OC=3����
OC=3���� ![]() ��
��
OP= ![]() ����OE=OP+PE=OP+OA=
����OE=OP+PE=OP+OA= ![]() +3=
+3= ![]() ��
��
��E�������ǣ� ![]() ��0��
��0��
��2��
�⣺���ı���PCOD��ƽ���ı��Σ�
��OC=PD��
�ڡ�AOC�͡�EPD�У�
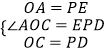 ��
��
���AOC�ա�EPD��
��AC=DE����CAO=��DEP��
��AC��DE��
���ı���ADEC��ƽ���ı���
��3��
�⣺C�������ǣ�0��6��2t����P�������ǣ�t��0������F�������ǣ�t+2��0������E�������ǣ�t+3��0����D�������ǣ�t��2t��6����
��CE�Ľ���ʽ��y=kx+b��
�� ![]() ��
��
��ã� 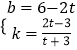 ��
��
��CE�Ľ���ʽ��y= ![]() ��
��
ͬ��DE�Ľ���ʽ��y= ![]() +
+ ![]() ��
��
��M��CE��ʱ��M�������ǣ�t+2�� ![]() ����
����
�� ![]() ��
��
��ã�t=21��12 ![]() ����t=1.5��
����t=1.5��
��N��DE���ǣ�N�������ǣ�t+2����1������ ![]() =��1��
=��1��
��ã�t=3+ ![]() ��t=9��
��t=9��
��֮�� ![]() ��t2=1.5��
��t2=1.5�� ![]() ��t4=9
��t4=9
����������1����C�˶���OB���е�ʱ������ʱ��t=·��/�ٶȼ�����ã��������E�����ꣻ��2��֤����AOC�ա�EPD����AC=DE����CAO=��DEP����AC��DEƽ������ȣ����ı���ADECΪƽ���ı��Σ���3�����ô���ϵ�������CE��DE�Ľ���ʽ��Ȼ����t��ʾ��M��N�����꣬�������ʽ�������t��ֵ��

����Ŀ������ijһ�ܵ����������ͳ�����±���
������£��棩 | 25 | 26 | 27 | 28 |
���� | 1 | 1 | 2 | 3 |
����ܵ���������µ���λ���������ֱ��ǣ�������
A. 26.5��27 B. 27��28 C. 27��27 D. 27.5��28
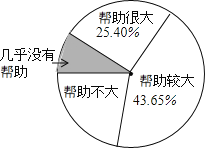
����Ŀ��Ϊ�˽⡰��ѧ˼�����Ķ�ѧϰ��ѧ�����ж��һ�о�Ա�����ȡ��һ�������ĸ�У��һѧ���������ʾ����飬��������õ������������������ͼ�ͱ�����ʾ��ͼ������û������ɣ���
ѡ�� | �����ܴ� | �����ϴ� | �������� | ����û�а��� |
���� | a | 543 | 269 | b |
����ͼ�����ṩ����Ϣ��
��1�����ʣ���ι��ж�����ѧ���������ʾ����飿
��2���������a��b��ֵ��
��ע���������漰���ġ�����������ȷ��1��