题目内容
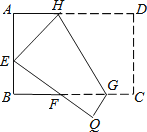
【题目】如图：EF∥AD ，∠1=∠2，∠BAC=70°，将求∠AGD的过程填写完整：
因为EF∥AD，所以∠2=＿＿
又因为∠1=∠2，所以∠1=∠3
所以AB∥＿＿
所以∠BAC+＿＿=180°
因为∠BAC=70°，所以∠AGD=＿＿
【答案】∠3 两直线平行，同位角相等
DG 内错角相等，两直线平行
∠AGD 110°
【解析】
根据平行线的性质和已知求出∠1=∠3，根据平行线的判定推出AB∥DG，根据平行线的性质求出∠BAC+∠DGA=180°即可．
∵EF∥AD
∴∠2=∠3（两直线平等，同位角相等）
又∵∠1=∠2
∴∠1=∠3（等量代换）
∴AB∥DG（内错角相等，两直线平等）
∴∠BAC+∠AGD=180°（两直线平等，同旁内角互补）
∵∠BAC=70°（已知）
∴∠AGD=180°-70°=110°（等量代换）
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
