题目内容
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,![]() 是直线
是直线![]() 在第一象限内的一个动点
在第一象限内的一个动点
(1)求⊿![]() 的面积
的面积![]() 与
与![]() 的函数解析式,并写出自变量
的函数解析式,并写出自变量![]() 的取值范围?
的取值范围?
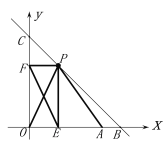
(2)过点![]() 作
作![]() 轴于点
轴于点![]() , 作
, 作![]() 轴于点
轴于点![]() ,连接
,连接![]() ,是否存在一点
,是否存在一点![]() 使得
使得![]() 的长最小,若存在,求出
的长最小,若存在,求出![]() 的最小值;若不存在,请说明理由 ?
的最小值;若不存在,请说明理由 ?
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 的最小值为
的最小值为![]()
【解析】本题的⑴问直接根据坐标来表示⊿![]() 的底边和底边上的高,利用三角形的面积公式得出函数解析式;
的底边和底边上的高,利用三角形的面积公式得出函数解析式;
本题的⑵抓住四边形![]() 是矩形,矩形的对角线相等即
是矩形,矩形的对角线相等即![]() ,从而把
,从而把![]() 转化到
转化到![]() 上来解决,当
上来解决,当![]() 的端点
的端点![]() 运动到
运动到![]() 时
时![]() 最短,以此为切入点,问题可获得解决.
最短,以此为切入点,问题可获得解决.
⑴.∵![]() 的坐标为
的坐标为![]() ,
,![]() 是直线
是直线![]() 在第一象限的一个动点,且
在第一象限的一个动点,且![]() 轴.
轴.
∴![]() ,
,![]()
∴![]() 整理得:
整理得:![]()
自变量![]() 的取值范围是:
的取值范围是:![]()
⑵. 存在一点![]() 使得
使得![]() 的长最小.
的长最小.
求出直线![]() 与
与![]() 轴交点的坐标为
轴交点的坐标为![]() , 与
, 与![]() 轴交点的坐标为
轴交点的坐标为![]()
∴![]() ∴
∴![]()
根据勾股定理计算:![]() .
.
∵![]() 轴,
轴, ![]() 轴,
轴,![]() 轴
轴![]()
![]() 轴
轴
∴![]()
∴四边形![]() 是矩形 ∴
是矩形 ∴![]()
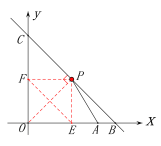
当![]() 的端点
的端点![]() 运动到
运动到![]() (实际上点
(实际上点![]() 恰好是
恰好是![]() 的中点)时
的中点)时
的![]() 最短(垂线段最短)(见示意图)
最短(垂线段最短)(见示意图)
又∵![]() ∴
∴![]() 点为线段
点为线段![]() 中点(三线合一)
中点(三线合一)
∴ ![]() (注:也可以用面积方法求解)
(注:也可以用面积方法求解)
∴![]() 即
即![]() 的最小值为
的最小值为![]()

练习册系列答案
相关题目