Question

【题目】在平面直角坐标系中，抛物线与轴交于A、B（A点在B点的左侧）与轴交于点C．

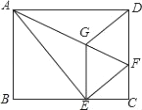
(1）如图１，连接AC、BC，若△ABC的面积为3时，求抛物线的解析式；

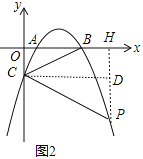
(2）如图2，点P为第四象限抛物线上一点，连接PC，若时，求点P的横坐标；

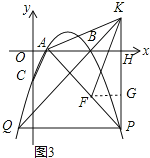
(3）如图3，在（2）的条件下，点F在AP上，过点P作PH⊥轴于H点，点K在PH的延长线上，AK＝KF，∠KAH=∠FKH，PF=，连接KB并延长交抛物线于点Q，求PQ的长.

Answer 1

【答案】（1）解析式为；（2）点P 的横坐标为6 ；

(3) QP=7

【解析】试题分析：（1）通过解方程ax2-5ax+4a=0可得到A（1，0），B（4，0），然后利用三角形面积公式求出OC得到C点坐标，再把C点坐标代入y=ax2-5ax+4a中求出a即可得到抛物线的解析式；

（2）过点P作PH⊥x轴于H，作CD⊥PH于点H，如图2，设P（x，ax2-5ax+4a），则PD=-ax2+5ax，通过证明Rt△PCD∽Rt△CBO，利用相似比可得到（-ax2+5ax）：（-4a）=x：4，然后解方程求出x即可得到点P的横坐标；

（3）过点F作FG⊥PK于点G，如图3，先证明∠HAP=∠KPA得到HA=HP，由于P（6，10a），则可得到-10a=6-1，解得a=-，再判断Rt△PFG单位等腰直角三角形得到FG=PG=PF=2，接着证明△AKH≌△KFG，得到KH=FG=2，则K（6，2），然后利用待定系数法求出直线KB的解析式为y=x-4，再通过解方程组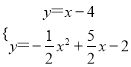得到Q（-1，-5），利用P、Q点的坐标可判断PQ∥x轴，于是可得到QP=7．

试题解析：（1）当y=0时，ax2-5ax+4a=0，解得x1=1，x2=4，则A（1，0），B（4，0），

∴AB=3，

∵△ABC的面积为3，

∴，解得OC=2，则C（0，-2），

把C（0，-2）代入y=ax2-5ax+4a得4a=-2，解得a=-，

∴抛物线的解析式为y=-x2+x-2；

（2）过点P作PH⊥x轴于H，作CD⊥PH于点H，如图2，设P（x，ax2-5ax+4a），则PD=4a-（ax2-5ax+4a）=-ax2+5ax，

∵AB∥CD，

∴∠ABC=∠BCD，

∵∠BCP=2∠ABC，

∴∠PCD=∠ABC，

∴Rt△PCD∽Rt△CO，

∴PD：OC=CD：OB，

即（-ax2+5ax）：（-4a）=x：4，解得x1=0，x2=6，

∴点P的横坐标为6；

（3）过点F作FG⊥PK于点G，如图3，

∵AK=FK，

∴∠KAF=∠KFA，

而∠KAF=∠KAH+∠PAH，∠KFA=∠PKF+∠KPF，

∵∠KAH=∠FKP，

∴∠HAP=∠KPA，

∴HA=HP，

∴△AHP为等腰直角三角形，

∵P（6，10a），

∴-10a=6-1，解得a=-，

在Rt△PFG中，∵PF=4a=2，∠FPG=45°，

∴FG=PG=PF=2，

在△AKH和△KFG中

，

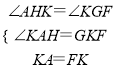∴△AKH≌△KFG，

∴KH=FG=2，

∴K（6，2），

设直线KB的解析式为y=mx+n，

把K（6，2），B（4，0）代入得

，

解得，

∴直线KB的解析式为y=x-4，

当a=-时，抛物线的解析式为y=-x2+x-2，

解方程组，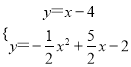

解得或，

∴Q（-1，-5），

而P（6，-5），

∴PQ∥x轴，

∴QP=7．