题目内容
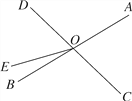
【题目】如图,直线AB与CD相交于点O,OE⊥AB,OF⊥CD,OP是∠BOC的平分线.
(1)请写出图中所有∠EOC的补角 ____________________;
(2)如果∠POC:∠EOC=2:5.求∠BOF的度数.

【答案】(1)∠EOD和∠AOF;(2)50°.
【解析】试题分析:(1)首先根据垂直定义可得∠AOE=∠DOF=90°,然后再证明∠EOD=∠AOF,根据补角定义可得∠EOD,∠AOF都是∠EOC的补角;
(2)根据角平分线定义可得∠POC=∠POB,再根据条件∠POC:∠EOC=2:5,可得∠COP的度数,然后即可算出∠BOF的度数.
试题解析:解:(1)∵OE⊥AB,OF⊥CD,∴∠AOE=∠DOF=90°,∴∠EOA+∠AOD=∠DOF+∠AOD,即:∠EOD=∠AOF,∵∠EOC+∠EOD=180°,∴∠AOF+∠EOC=180°,∴∠EOD,∠AOF都是∠EOC的补角,故答案为:∠EOD,∠AOF;
(2)∵OP是∠BOC的平分线,∴∠POC=∠POB,∵∠POC:∠EOC=2:5,∴∠POC=90°×![]() =20°,∴∠POB=20°,∵∠DOF=90°,∴∠BOF=90°﹣20°﹣20°=50°.
=20°,∴∠POB=20°,∵∠DOF=90°,∴∠BOF=90°﹣20°﹣20°=50°.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
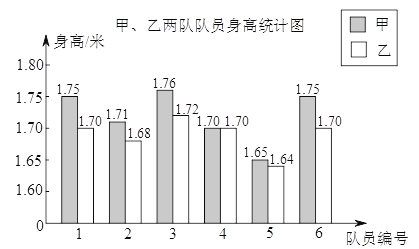
【题目】某学校要成立一支由6名女生组成的礼仪队,八年级两个班各选6名女生,分别组成甲队和乙队参加选拔.每位女生的身高统计如图,部分统计量如下表:
平均数 | 标准差 | 中位数 | |
甲队 | 1.72 | 0.038 | |
乙队 | 0.025 | 1.70 |
(1)求甲队身高的中位数;
(2)求乙队身高的平均数及身高不小于1.70米的频率;
(3)如果选拔的标准是身高越整齐越好,那么甲、乙两队
中哪一队将被录取?请说明理由.