题目内容
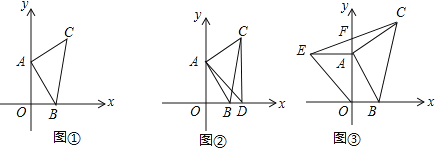
【题目】两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.
(1)求证:△ABE≌△ACD;
(2)求证:DC⊥BE.

【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)根据等腰直角三角形的性质,可以得出△ABE≌△ACD;
(2)由△ABE≌△ACD可以得出∠B=∠ACD﹣45°,进而得出∠DCB=90°,就可以得出结论.
证明:(1)∵△ABC与△AED均为等腰直角三角形,
∴AB=AC,AE=AD,∠BAC=∠EAD=90°.∠ABC=∠ACB=45°,
∴∠BAC+∠CAE=∠EAD+∠CAE.
即∠BAE=∠CAD,
在△ABE与△ACD中,
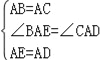 ,
,
∴△ABE≌△ACD(SAS),
(2)证明:∵△ABE≌△ACD,
∴∠ACD=∠ABE=45°,
又∵∠ACB=45°,
∴∠BCD=∠ACB+∠ACD=90°,
∴DC⊥BE.
点睛:此题主要考查了等腰直角三角形的性质以及全等三角形的性质与判定,根据等腰三角形的性质得出AC=AB,AD=AE,利用SAS证全等是解题关键.

练习册系列答案
相关题目