题目内容
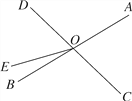
【题目】如图,直线AB、CD相交于点O,OE把∠BOD分成两部分.
(1)图中∠AOC的对顶角为________,∠BOE的补角为________;
(2)若∠AOC=75°,且∠BOE∶∠EOD=1∶4,求∠AOE的度数.
【答案】 ∠BOD ∠AOE
【解析】试题分析:(1)利用对顶角、邻补角的定义直接回答即可;
(2)根据对顶角相等求出∠BOD的度数,再根据∠BOE:∠EOD=1:4求出∠BOE的度数,然后利用互为邻补角的两个角的和等于180°即可求出∠AOE的度数.
试题解析:
解:(1)∠BOD ∠AOE
(2)∵∠DOB=∠AOC=75°,∠DOB=∠BOE+∠EOD,
∠BOE∶∠EOD=1∶4,
∴∠EOD=4∠BOE,
∴∠BOE+4∠BOE=75°,
∴∠BOE=15°,
∴∠AOE=180°-∠BOE=165°.

练习册系列答案
相关题目