题目内容
【题目】已知二次函数y=ax2+bx+c（a＞0）的图象与x轴交于A（x1，0）、B（x2，0）（x1＜x2）两点，与y轴交于点C，x1，x2是方程x2+4x﹣5=0的两根．
（1）若抛物线的顶点为D，求S△ABC：S△ACD的值；
（2）若∠ADC=90°，求二次函数的解析式．
【答案】（1）1：1；（2）y=
x2+
x﹣
．
【解析】
试题分析：（1）首先解一元二次方程，求出点A、点B的坐标，得到含有字母a的抛物线的交点式；然后分别用含字母a的代数式表示出△ABC与△ACD的面积，最后得出结论；
（2）在Rt△ACD中，利用勾股定理，列出一元二次方程，求出未知系数a，得出抛物线的解析式．
试题解析：（1）解方程x2+4x-5=0，得x=-5或x=1，
由于x1＜x2，则有x1=-5，x2=1，
∴A（-5，0），B（1，0）．
抛物线的解析式为：y=a（x+5）（x-1）（a＞0），
∴对称轴为直线x=-2，顶点D的坐标为（-2，-9a），
令x=0，得y=-5a，
∴C点的坐标为（0，-5a）．
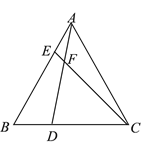
依题意画出图形，如右图所示，则OA=5，OB=1，AB=6，OC=5a，
过点D作DE⊥y轴于点E，则DE=2，OE=9a，CE=OE-OC=4a．
S△ACD=S梯形ADEO-S△CDE-S△AOC
=
（DE+OA）OE-DECE-OAOC=（2+5）9a-×2×4a-×5×5a=15a，
而S△ABC=ABOC=×6×5a=15a，
∴S△ABC：S△ACD=15a：15a=1：1；
（2）如解答图，过点D作DE⊥y轴于E
在Rt△DCE中，由勾股定理得：CD2=DE2+CE2=4+16a2，
在Rt△AOC中，由勾股定理得：AC2=OA2+OC2=25+25a2，
设对称轴x=-2与x轴交于点F，则AF=3，
在Rt△ADF中，由勾股定理得：AD2=AF2+DF2=9+81a2．
∵∠ADC=90°，∴△ACD为直角三角形，
由勾股定理得：AD2+CD2=AC2，
即（9+81a2）+（4+16a2）=25+25a2，化简得：a2=
，
∵a＞0，
∴a=，
∴抛物线的解析式为：y=
（x+5）（x﹣1）=
x2+x﹣．
考点: 二次函数综合题．
