题目内容
如图所示,C、D是线段AB上的两点,AB=a,CD=b,M、N、P分别为AC、CD、D B的中点,
B的中点,
(1)求AM+CN+DP的长
(2)求AM+PB的长
(3)求PM的长.
 B的中点,
B的中点,(1)求AM+CN+DP的长
(2)求AM+PB的长
(3)求PM的长.
分析:(1)根据中点定义分别表示出AM、CN、DP,整理即可得解;
(2)根据中点定义分别表示出AM、PB,整理即可得到AM+PB的长等于(AB-CD)的一半;
(3)用AB减去(AM+PB)的长即可.
(2)根据中点定义分别表示出AM、PB,整理即可得到AM+PB的长等于(AB-CD)的一半;
(3)用AB减去(AM+PB)的长即可.
解答:解:(1)∵M、N、P分别为AC、CD、DB的中点,
∴AM=
AC,CN=
CD,DP=
DB,
∴AM+CN+DP=
(AC+CD+DB)=
AB,
∵AB=a,
∴AM+CN+DP=
a;
(2)∵M、P分别为AC、DB的中点,
∴AM=
AC,PB=
DB,
∴AM+PB=
(AC+DB)=
(AC+CD+DB-CD)=
AB-
CD,
∵AB=a,CD=b,
∴AM+PB=
a-
b;
(3)根据图形可知,PM=AB-(AM+PB),
∵AB=a,AM+PB=
a-
b,
∴PM=a-(
a-
b)=a-
a+
b=
a+
b.
∴AM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴AM+CN+DP=
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=a,
∴AM+CN+DP=
| 1 |
| 2 |
(2)∵M、P分别为AC、DB的中点,
∴AM=
| 1 |
| 2 |
| 1 |
| 2 |
∴AM+PB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=a,CD=b,
∴AM+PB=
| 1 |
| 2 |
| 1 |
| 2 |
(3)根据图形可知,PM=AB-(AM+PB),
∵AB=a,AM+PB=
| 1 |
| 2 |
| 1 |
| 2 |
∴PM=a-(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了两点间的距离的求解,主要利用了线段中点的定义,根据中点理清图中各线段之间的关系是解题的关键.

练习册系列答案
相关题目

 如图所示,A、B是4×5网格中的格点(网格线的交点),网格中的每个小正方形的边长都是1.
如图所示,A、B是4×5网格中的格点(网格线的交点),网格中的每个小正方形的边长都是1. 23、如图所示,已知O是∠EPF的平分线上的一点,以O为圆心的圆与角的两边分别交于点A、B和C、D.
23、如图所示,已知O是∠EPF的平分线上的一点,以O为圆心的圆与角的两边分别交于点A、B和C、D.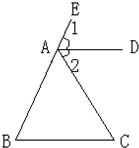 如图所示,已知AD是∠EAC的平分线,且AD∥BC,求证:∠B=∠C.
如图所示,已知AD是∠EAC的平分线,且AD∥BC,求证:∠B=∠C.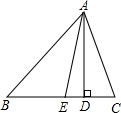 如图所示,AD,AE是三角形ABC的高和角平分线,∠B=36°,∠C=76°,求∠DAE的度数.
如图所示,AD,AE是三角形ABC的高和角平分线,∠B=36°,∠C=76°,求∠DAE的度数.