题目内容
 23、如图所示,已知O是∠EPF的平分线上的一点,以O为圆心的圆与角的两边分别交于点A、B和C、D.
23、如图所示,已知O是∠EPF的平分线上的一点,以O为圆心的圆与角的两边分别交于点A、B和C、D.(1)求证:PB=PD;
(2)若角的顶点P在圆上或圆内,(1)中的结论还成立吗?若不成立,请说明理由;若成立,请加以证明.
分析:(1)过O作OE⊥PB于E,OF⊥PD于F.根据角平分线的性质可知OE=OF,PE=PF,再利用全等三角形的性质证明.
(2)成立,证明的理论依据相同.
(2)成立,证明的理论依据相同.
解答:解:(1)证明:过O作OE⊥PB于E,OF⊥PD于F.
∵OP平分∠EPF,
∴OE=OF,又OP=OP,
∴Rt△POE≌Rt△POF(HL),
∴PE=PF,
∴AB=CD,则BE=DF,
∴PE+BE=PF+DF,
∴PB=PD.

(2)上述结论仍成立.如下图所示.证明略.
当点P在圆上时,
根据解平分线的性质可知OE=OF,
∴△OPE≌△OPF,
∴PE=PF,
根据垂径定理得AE=PE,CF=PF,
∴AP=CP,
当点P在圆内时,
根据解平分线的性质可知OE=OF,
∴△OPE≌△OPF,
∴PE=PF,
连接OA,OC则△OAE≌△OCF,
∴AE=CF,
∴AP=CP.
∵OP平分∠EPF,
∴OE=OF,又OP=OP,
∴Rt△POE≌Rt△POF(HL),
∴PE=PF,
∴AB=CD,则BE=DF,
∴PE+BE=PF+DF,
∴PB=PD.

(2)上述结论仍成立.如下图所示.证明略.
当点P在圆上时,
根据解平分线的性质可知OE=OF,
∴△OPE≌△OPF,
∴PE=PF,
根据垂径定理得AE=PE,CF=PF,
∴AP=CP,
当点P在圆内时,
根据解平分线的性质可知OE=OF,
∴△OPE≌△OPF,
∴PE=PF,
连接OA,OC则△OAE≌△OCF,
∴AE=CF,
∴AP=CP.
点评:本题综合考查了垂径定理和全等三角形的判定及性质.注意做几何题时一定要图题结合,利用图形来直观形象的解题.

练习册系列答案
相关题目
 22、如图所示,已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速运动,其中点P运动的速度是1m/s,点Q运动的速度是2m/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t s,解答下列问题:
22、如图所示,已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速运动,其中点P运动的速度是1m/s,点Q运动的速度是2m/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t s,解答下列问题: 19、如图所示,已知O是四边形ABCD内一点,OB=OC=OD,∠BCD=∠BAD=75°,则∠ADO+∠ABO=
19、如图所示,已知O是四边形ABCD内一点,OB=OC=OD,∠BCD=∠BAD=75°,则∠ADO+∠ABO=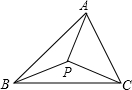 如图所示,已知P是△ABC内一点,试说明PA+PB+PC>
如图所示,已知P是△ABC内一点,试说明PA+PB+PC>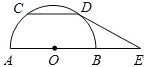 如图所示,已知AB是半圆O的直径,弦CD∥AB,AB=10,CD=6,E是AB延长线上一点,BE=
如图所示,已知AB是半圆O的直径,弦CD∥AB,AB=10,CD=6,E是AB延长线上一点,BE= 20、如图所示,已知AB是半圆O的直径,∠BAC=22°,则∠B=
20、如图所示,已知AB是半圆O的直径,∠BAC=22°,则∠B=