Question

如图所示，A、B是4×5网格中的格点（网格线的交点），网格中的每个小正方形的边长都是1．
（1）请在图中标出使以A、B、C为顶点的三角形是等腰三角形的所有格点C的位置（分别用C₁、C₂、C₃依次标出）．
（2）若以点A为坐标原点建立平面直角坐标系，求直线BC的解析式．（只需求一条即可）

Answer 1

分析：（1）AB=

13

，分三种情况：当AC=AB时；当BC=AC时，当AC=BC时；
（2）设出BC直线的解析式，用待定系数法可确定出k，b的值．

解答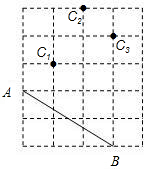：解：（1）如图所示，点C共有三种可能位置．

（2）依题意得：点B（3，-2），点C₁（1，1），
设直线的解析式为y=kx+b，则：

3k+b=-2 k+b=1

，
解得

k=- 3 2 b= 5 2

，
∴所求直线解析式为y=-

3

2

x+

5

2

，
若选点C₂（2，3），则所求直线解析式为y=-5x+13，
若选点C₃（3，2），
∵点B（3，-2）点C₃（3，2）在平行于y轴的直线上，
∴直线解析式为直线x=3．

点评：本题考查了等腰三角形的性质和用待定系数法确定直线的解析式．